题目内容
3.已知a>0,b>0,若不等式$a+b≥\frac{mab}{a+4b}$恒成立,则m的最大值等于( )| A. | 10 | B. | 9 | C. | 8 | D. | 7 |
分析 a>0,b>0,不等式$a+b≥\frac{mab}{a+4b}$恒成立,m≤$\frac{(a+b)(a+4b)}{ab}$的最小值,利用基本不等式的性质即可得出.
解答 解:∵a>0,b>0,不等式$a+b≥\frac{mab}{a+4b}$恒成立,
∴m≤$\frac{(a+b)(a+4b)}{ab}$的最小值,
而$\frac{(a+b)(a+4b)}{ab}$=$\frac{{a}^{2}+4{b}^{2}+5ab}{ab}$≥$\frac{4ab+5ab}{ab}$=9,当且仅当a=2b>0时取等号.
∴m≤9,
∴m的最大值等于9.
故选:B.
点评 本题考查了恒成立等价转化问题、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
15.定义点P(x0,y0)到直线l:ax+by+c=0(a2+b2≠0)的有向距离为d=$\frac{{a{x_0}+b{y_0}+c}}{{\sqrt{{a^2}+{b^2}}}}$.已知点P1、P2到直线l的有向距离分别是d1、d2.以下命题正确的是( )
| A. | 若d1-d2=0,则直线P1P2与直线l平行 | |
| B. | 若d1+d2=0,则直线P1P2与直线l平行 | |
| C. | 若d1+d2=0,则直线P1P2与直线l垂直 | |
| D. | 若d1•d2<0,则直线P1P2与直线l相交 |
12.圆(x-3)2+(y-3)2=9上到直线3x+4y-11=0的距离等于2的点有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
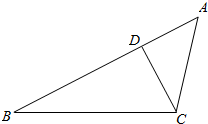 如图,在△ABC中,∠B=30°,AC=2$\sqrt{5}$,D是边AB上一点.
如图,在△ABC中,∠B=30°,AC=2$\sqrt{5}$,D是边AB上一点.