题目内容
18．某几何体的三视图如图所示．则该几何体的体积等于（ ）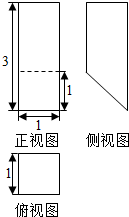
| A． | $\frac{3}{2}$ | B． | 2 | C． | $\frac{5}{2}$ | D． | 3 |
分析 几何体为四棱柱与三棱柱的组合体．
解答 解：由三视图可知该几何体上部分为四棱柱，下部分为三棱柱，四棱柱的底面为边长为1的正方形，高为2，三棱柱的底面为等腰直角三角形，直角边为1，三棱柱的高为1，
所以几何体的体积V=1×1×2+$\frac{1}{2}×1×1×1$=$\frac{5}{2}$．
故选C．
点评 本题考查了空间几何体的三视图与结构特征，几何体体积计算，属于基础题．
练习册系列答案
相关题目
8．设有一组圆Ck：（x-k+1）2+（y-3k）2=2k2（k∈N*）．下列四个命题：
①存在一条定直线与所有的圆均相切；
②存在一条定直线与所有的圆均相交；
③存在一条定直线与所有的圆均不相交；
④所有的圆均不经过原点．
其中真命题的序号是（ ）
①存在一条定直线与所有的圆均相切；
②存在一条定直线与所有的圆均相交；
③存在一条定直线与所有的圆均不相交；
④所有的圆均不经过原点．
其中真命题的序号是（ ）
| A． | ①③ | B． | ②④ | C． | ②③ | D． | ③④ |
13．2015年高考体检中，某校高三共有学生1000人，检查的身体的某项指标为由低到高的4个等级，具体如下表：
（1）若按分层抽样的方法从中抽取20人，再从这20人中抽取2人，求这2人的该项身体指标级别至少有1人小于2人的概率；
（2）若把该校高三学生该项指标中恰好为1级的频率视为概率，从这1000人中任选1人，若其该项指标恰好为1级则结束，否则再选取1人，依次选取，直至找到1人该项指标恰好为1级或选够4人，则结束选取，求结束时选取的人数的分布列与期望．
| 等级 | 1级 | 2级 | 3级 | 4级 |
| 人数 | 200 | 500 | 200 | 100 |
（2）若把该校高三学生该项指标中恰好为1级的频率视为概率，从这1000人中任选1人，若其该项指标恰好为1级则结束，否则再选取1人，依次选取，直至找到1人该项指标恰好为1级或选够4人，则结束选取，求结束时选取的人数的分布列与期望．
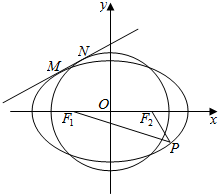如图，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F1、F2，P为椭圆C上任意一点，当|PF1|-|PF2|取最大值时，|PF1|=3，|PF2|=1．