题目内容
9.在△ABC中,a,b,c分别为内角A,B,C的对边,已知C为锐角且$\sqrt{15}$asinA=bsinBsinC,b=2a.(1)求tanC的值;
(2)求$\frac{c}{a}$的值.
分析 (1)由已知,根据正弦定理化简已知等式可求sinC,利用同角三角函数基本关系式可求cosC,tanC的值.
(2)由余弦定理可得:c2=a2+b2-2abcosC=4a2,即可得解$\frac{c}{a}=2$.
解答 (本题满分为12分)
解:(1)由已知,根据正弦定理可得:$\sqrt{15}$a2=b2sinC=4a2sinC,
∴sinC=$\frac{\sqrt{15}}{4}$,cosC=$\frac{1}{4}$,
∴tanC=$\frac{sinC}{cosC}$=$\sqrt{15}$…6分
(2)由余弦定理可得:c2=a2+b2-2abcosC=5a2-4a2×$\frac{1}{4}$=4a2,
解得:$\frac{c}{a}=2$…12分
点评 本题主要考查了正弦定理,余弦定理,同角三角函数基本关系式在解三角形中的应用,属于基础题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
19.直线ax-2by+1=0(a>0,b>0)平分圆x2+y2+4x-2y-1=0的面积,则$\frac{1}{a}$+$\frac{2}{b}$的最小值为( )
| A. | 3+2$\sqrt{2}$ | B. | 4+2$\sqrt{3}$ | C. | 6+4$\sqrt{2}$ | D. | 8$\sqrt{3}$ |
1.两平行线3x-4y-2=0与3x-4y+8=0之间的距离为( )
| A. | 2 | B. | $\frac{6}{5}$ | C. | 1 | D. | 2$\sqrt{5}$ |
18.某几何体的三视图如图所示.则该几何体的体积等于( )
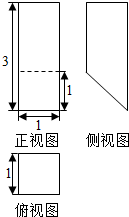

| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
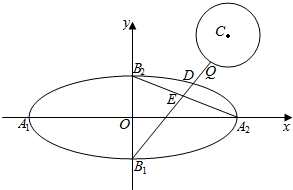 如图,已知椭圆$\frac{{x}^{2}}{2}$+y2=1的四个顶点分别为A1,A2,B1,B2,左右焦点分别为F1,F2,若圆C:(x-3)2+(y-3)2=r2(0<r<3)上有且只有一个点P满足$\frac{|P{F}_{1}|}{|P{F}_{2}|}$=$\sqrt{5}$.
如图,已知椭圆$\frac{{x}^{2}}{2}$+y2=1的四个顶点分别为A1,A2,B1,B2,左右焦点分别为F1,F2,若圆C:(x-3)2+(y-3)2=r2(0<r<3)上有且只有一个点P满足$\frac{|P{F}_{1}|}{|P{F}_{2}|}$=$\sqrt{5}$.