题目内容
8.A={x|2x2-px+q=0},B={x|6x2+(p+2)x+q=0},若A∩B={2}.(1)求p,q的值;
(2)求A∪B.
分析 由条件便知2为方程2x2-px+q=0和方程6x2+(p+2)x+q=0的解,带入方程便可求出p,q,从而可解出这两个方程,然后进行并集的运算即可.
解答 解:(1)∵A∩B={2}.
∴2∈A,2∈B,
∴$\left\{\begin{array}{l}{8-2p+q=0}\\{24+2(p+2)+q=0}\end{array}\right.$,
解得p=-5,q=-18;
(2)∵A={x|2x2+5x-18=0}={-$\frac{9}{2}$,2},B={x|6x2-3x-18=0}={-$\frac{3}{2}$,2},
∴A∪B={-$\frac{9}{2}$,-$\frac{3}{2}$,2},
点评 考查交集的概念,元素与集合的关系,解一元二次方程,以及并集的运算.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
18.某几何体的三视图如图所示.则该几何体的体积等于( )
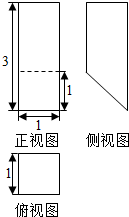

| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
19.已知向量$\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(-1,2),若$\overrightarrow{a}$-2$\overrightarrow{b}$与非零向量m$\overrightarrow{a}$+n$\overrightarrow{b}$共线,则$\frac{m}{n}$等于( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
16.曲线y=$\frac{1}{5}$x5上一点M处的切线与直线y=3-x垂直,则此切线方程可能为( )
| A. | 5x-5y-4=0 | B. | 5x-5y+4=0. | C. | 5x+5y-4=0 | D. | 3x+5y-4=0 |
20.若a,b,c是△ABC的三边,若直线ax+by+c=0与圆x2+y2=1无公共点,则△ABC的形状是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 不能确定 |