题目内容

10．如图，在长方体ABCD-A1B1C1D1中，F，G分别是CC1，BC两边的中点，画出平面D1FG与平面ABCD的交线．

分析 连结AD1、AG，则AG是平面D1FG与平面ABCD的交线．

解答 解：连结AD1、AG，则AG是平面D1FG与平面ABCD的交线．
证明如下：
∵在长方体ABCD-A1B1C1D1中，F，G分别是CC1，BC两边的中点，
∴FG∥BC1，
又BC1∥AD1，∴FG∥AD1，
∴A、G、F、D1四点共面于平面D1FG，
∵AG?平面ABCD，
∴AG是平面D1FG与平面ABCD的交线．

点评 本题考查面面交线的画法，是基础题，解题时要认真审题，注意空间思维能力的培养．

练习册系列答案
相关题目
20．在△ABC中，角A，B，C的对边分別a，b，c，且3csinA=bsinC 
（1）求$\frac{b}{a}$的值；
（2）若△ABC的面积为3$\sqrt{3}$，且C=60°，求c的值．
1．两平行线3x-4y-2=0与3x-4y+8=0之间的距离为（　　）
A．2B．$\frac{6}{5}$C．1D．2$\sqrt{5}$
18．某几何体的三视图如图所示．则该几何体的体积等于（　　）
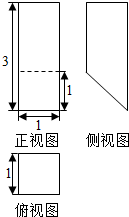
A．$\frac{3}{2}$B．2C．$\frac{5}{2}$D．3
5．函数y=$\frac{1}{{x}^{4}}$，则y′=-$\frac{4}{{x}^{5}}$．
15．已知函数f（x）=-asinx+b，（a，b∈R）．
（1）若a＞0，当x∈[-$\frac{π}{2}$，$\frac{π}{6}$]时，函数f（x）的最大值为0，最小值为-4，求a，b的值；
（2）当b=1，函数g（x）=f（x）+cos2x，x∈[$\frac{π}{6}$，$\frac{7π}{6}$]的最大值为3，求a的值．
2．设△ABC内角A，B，C的对边分别为a，b，c．已知sin2A一sin2B=sinC（sinC一sinB）．
（1）求角A的值．
（2）若b+c=1，求a的取值范围．
19．已知向量$\overrightarrow{a}$=（2，3），$\overrightarrow{b}$=（-1，2），若$\overrightarrow{a}$-2$\overrightarrow{b}$与非零向量m$\overrightarrow{a}$+n$\overrightarrow{b}$共线，则$\frac{m}{n}$等于（　　）
A．-2B．2C．-$\frac{1}{2}$D．$\frac{1}{2}$
20．若a，b，c是△ABC的三边，若直线ax+by+c=0与圆x2+y2=1无公共点，则△ABC的形状是（　　）
A．锐角三角形B．钝角三角形C．直角三角形D．不能确定

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网