题目内容
6.已知定义在($\frac{2}{3}$,+∞)的函数f(x)满足f(x+1)-f(x)=log3(x-$\frac{2}{3}$),若f(1)=2,则f(2)=1.分析 根据抽象函数关系,利用赋值法进行求解即可.
解答 解:∵定义在($\frac{2}{3}$,+∞)的函数f(x)满足f(x+1)-f(x)=log3(x-$\frac{2}{3}$),且f(1)=2,
∴当x=1时,f(2)-f(1)=log3(1-$\frac{2}{3}$)=log3$\frac{1}{3}$=-1,
即f(2)=-1+f(1)=-1+2=1,
则f(2)=1,
故答案为:1.
点评 本题主要考查函数值的计算,利用抽象函数关系利用赋值法是解决本题的关键.比较基础.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
1.两平行线3x-4y-2=0与3x-4y+8=0之间的距离为( )
| A. | 2 | B. | $\frac{6}{5}$ | C. | 1 | D. | 2$\sqrt{5}$ |
11.一个人将编号为1,2,3,4的四个小球随机放入编号为1,2,3,4的四个盒子中,每个盒子放一个小球,球的编号与盒子的编号相同时叫做放对了,否则叫做错了,设放对的个数为ξ,则ξ的期望值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
18.某几何体的三视图如图所示.则该几何体的体积等于( )
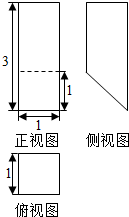

| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
16.曲线y=$\frac{1}{5}$x5上一点M处的切线与直线y=3-x垂直,则此切线方程可能为( )
| A. | 5x-5y-4=0 | B. | 5x-5y+4=0. | C. | 5x+5y-4=0 | D. | 3x+5y-4=0 |
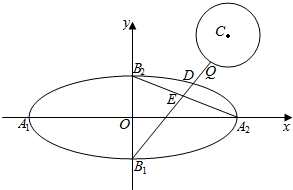 如图,已知椭圆$\frac{{x}^{2}}{2}$+y2=1的四个顶点分别为A1,A2,B1,B2,左右焦点分别为F1,F2,若圆C:(x-3)2+(y-3)2=r2(0<r<3)上有且只有一个点P满足$\frac{|P{F}_{1}|}{|P{F}_{2}|}$=$\sqrt{5}$.
如图,已知椭圆$\frac{{x}^{2}}{2}$+y2=1的四个顶点分别为A1,A2,B1,B2,左右焦点分别为F1,F2,若圆C:(x-3)2+(y-3)2=r2(0<r<3)上有且只有一个点P满足$\frac{|P{F}_{1}|}{|P{F}_{2}|}$=$\sqrt{5}$.