题目内容
根据下列条件解三角形：
（1）b=
，B=60°，c=1；
（2）c=
，A=45°，a=2．
（1）b=
| 3 |
（2）c=
| 6 |
考点：解三角形的实际应用
专题：解三角形
分析：根据正弦定理，结合三角形的边角关系即可求出三角形的边长．
解答：
解：（1）
=
，∴sinC=
=
=
，
∵b＞c，B=60°，∴C＜B，∴C为锐角，∴C=30°，A=90°，∴a=
=2．
（2）∵
=
，∴sinC=
=
=
，∴C=60°或120°，
∴当C=60°时，B=75°，b=
=
=
+1；
∴当C=120°时，B=15°，b=
=
=
-1；
∴b=
+1，B=75°，C=60°或b=
-1，B=15°，C=120°．
| b |
| sinB |
| c |
| sinC |
| csinB |
| b |
| 1×sin60° | ||
|
| 1 |
| 2 |
∵b＞c，B=60°，∴C＜B，∴C为锐角，∴C=30°，A=90°，∴a=
| b2+c2 |
（2）∵
| a |
| sinA |
| c |
| sinC |
| csinA |
| a |
| ||
| 2 |
| ||
| 2 |
∴当C=60°时，B=75°，b=
| csinB |
| sinC |
| ||
| sin60° |
| 3 |
∴当C=120°时，B=15°，b=
| csinB |
| sinC |
| ||
| sin120° |
| 3 |
∴b=
| 3 |
| 3 |
点评：本题主要考查正弦定理的应用，利用正弦定理是解决本题的关键．
练习册系列答案
相关题目
在△ABC中，AB=2，AC=1，D为BC边上的中点，∠BAD=30°，则AD的长为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
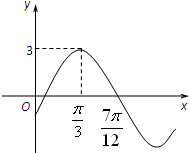已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
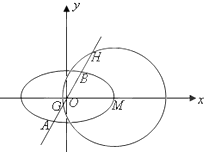已知圆M：（x-