题目内容
已知曲线C:y=eax.
(Ⅰ)若曲线C在点(0,1)处的切线为y=2x+m,求实数a和m的值;
(Ⅱ)对任意实数a,曲线C总在直线l:y=ax+b的上方,求实数b的取值范围.
(Ⅰ)若曲线C在点(0,1)处的切线为y=2x+m,求实数a和m的值;
(Ⅱ)对任意实数a,曲线C总在直线l:y=ax+b的上方,求实数b的取值范围.
考点:导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)根据导数的几何意义,y=eax在x=0处的切线方程为y-1=y′(0)x,再比较已知条件,可得;
(Ⅱ)原题意可转化为对于?x,a∈R,eax>ax+b恒成立,法1:进一步转化为?x,a∈R,eax-ax-b>0恒成立,令g(x)=eax-ax-b,分别从a=0和a≠0两种情况通过求导的方式进一步分析;法2:进一步转化为?x,a∈R,b<eax-ax恒成立,再令t=ax,则等价于?t∈R,b<et-t恒成立,再通过研究函数g(t)=et-t的性质求解.
(Ⅱ)原题意可转化为对于?x,a∈R,eax>ax+b恒成立,法1:进一步转化为?x,a∈R,eax-ax-b>0恒成立,令g(x)=eax-ax-b,分别从a=0和a≠0两种情况通过求导的方式进一步分析;法2:进一步转化为?x,a∈R,b<eax-ax恒成立,再令t=ax,则等价于?t∈R,b<et-t恒成立,再通过研究函数g(t)=et-t的性质求解.
解答:
解:(Ⅰ)y'=aeax,
因为曲线C在点(0,1)处的切线为L:y=2x+m,
所以1=2×0+m且y'|x=0=2.
解得m=1,a=2
(Ⅱ)法1:对于任意实数a,曲线C总在直线的y=ax+b的上方,等价于
?x,a∈R,都有eax>ax+b,
即?x,a∈R,eax-ax-b>0恒成立,
令g(x)=eax-ax-b,
①若a=0,则g(x)=1-b,
所以实数b的取值范围是b<1;
②若a≠0,g'(x)=a(eax-1),
由g'(x)=0得x=0,g'(x),g(x)的情况如下:
所以g(x)的最小值为g(0)=1-b,
所以实数b的取值范围是b<1;
综上,实数b的取值范围是b<1.
法2:对于任意实数a,曲线C总在直线的y=ax+b的上方,等价于
?x,a∈R,都有eax>ax+b,即
?x,a∈R,b<eax-ax恒成立,
令t=ax,则等价于?t∈R,b<et-t恒成立,
令g(t)=et-t,则 g'(t)=et-1,
由g'(t)=0得t=0,g'(t),g(t)的情况如下:
所以 g(t)=et-t的最小值为g(0)=1,
实数b的取值范围是b<1.
因为曲线C在点(0,1)处的切线为L:y=2x+m,
所以1=2×0+m且y'|x=0=2.
解得m=1,a=2
(Ⅱ)法1:对于任意实数a,曲线C总在直线的y=ax+b的上方,等价于
?x,a∈R,都有eax>ax+b,
即?x,a∈R,eax-ax-b>0恒成立,
令g(x)=eax-ax-b,
①若a=0,则g(x)=1-b,
所以实数b的取值范围是b<1;
②若a≠0,g'(x)=a(eax-1),
由g'(x)=0得x=0,g'(x),g(x)的情况如下:
| x | (-∞,0) | 0 | (0,+∞) |
| g'(x) | - | 0 | + |
| g(x) | ↘ | 极小值 | ↗ |
所以实数b的取值范围是b<1;
综上,实数b的取值范围是b<1.
法2:对于任意实数a,曲线C总在直线的y=ax+b的上方,等价于
?x,a∈R,都有eax>ax+b,即
?x,a∈R,b<eax-ax恒成立,
令t=ax,则等价于?t∈R,b<et-t恒成立,
令g(t)=et-t,则 g'(t)=et-1,
由g'(t)=0得t=0,g'(t),g(t)的情况如下:
| t | (-∞,0) | 0 | (0,+∞) |
| g'(t) | - | 0 | + |
| g(t) | ↘ | 极小值 | ↗ |
实数b的取值范围是b<1.
点评:本题中的导数的几何意义和利用导数研究函数的性质,是高考中经常考查的知识点和方法,特别是第二小问,通过数形转化后,对于“?x,a∈R,eax-ax-b>0恒成立,”的处理介绍了两种方法,对于拓宽学生的思维,拓展学生的思路有一定的指导作用,不过不管是哪种方法,最终都需要用导数的知识来进一步分析.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积为( )


| A、92+14π |
| B、92+24π |
| C、80+10π |
| D、80+20π |
求值:sin150°=( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
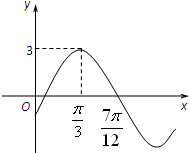 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<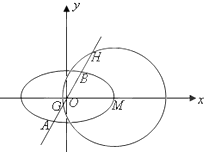 已知圆M:(x-
已知圆M:(x-