题目内容
已知点P(1,a)和圆x2+y2=4.
(1)若过点P的圆的切线只有一条,求a的值及切线方程;
(2)若a=
,过点P的圆的两条弦AC、BD互相垂直,求四边形ABCD面积的最大值.
(1)若过点P的圆的切线只有一条,求a的值及切线方程;
(2)若a=
| 2 |
考点:圆的切线方程,直线与圆的位置关系
专题:直线与圆
分析:(1)若过点P的圆的切线只有一条,则P在圆上,根据条件即可求a的值及切线方程;
(2)根据过点P的圆的两条弦AC、BD互相垂直,得到AC、BD的方程关系即可得到结论.
(2)根据过点P的圆的两条弦AC、BD互相垂直,得到AC、BD的方程关系即可得到结论.
解答:
解:(1)若过点P的圆的切线只有一条,则知点P圆上,
则1+a2=4,解得a=±
;
当a=
时,点P(1,
),切线方程为x+
y-4=0,
当a=-
时,点P(1,-
),切线方程为x-
y-4=0,
(2)设原点O到AC、BD的距离为d1,d2,(d1≥0,d2≥0)
则d12+d22=|OP|2=3,
于是|AC|=2
,|BD|=2
,
由AC、BD相互垂直,则四边形ABCD的面积
S=
|AC|•|BD|=2
=2
=2
,
∵d12+d22≥2d1d2,则d1d2≤
,当且仅当d1=d2=
时取“=”
则d12d22≤
,从而S=2
≤5,
即:四边形ABCD的面积最大值为5.
则1+a2=4,解得a=±
| 3 |
当a=
| 3 |
| 3 |
| 3 |
当a=-
| 3 |
| 3 |
| 3 |
(2)设原点O到AC、BD的距离为d1,d2,(d1≥0,d2≥0)
则d12+d22=|OP|2=3,
于是|AC|=2
| 4-d12 |
| 4-d22 |
由AC、BD相互垂直,则四边形ABCD的面积
S=
| 1 |
| 2 |
| (4-d12)(4-d22) |
| 16-4(d12+d22)+d12d22 |
| 4+d12d22 |
∵d12+d22≥2d1d2,则d1d2≤
| 3 |
| 2 |
| ||
| 2 |
则d12d22≤
| 9 |
| 4 |
| 4+d12d22 |
即:四边形ABCD的面积最大值为5.
点评:本题主要考查圆的切线方程以及直线和圆的位置关系,综合性较强,有一点难度.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
函数f(x)=
,若f(2)+f(α)=e+1,则α的所有可能值为( )
|
| A、1 | ||||
B、-
| ||||
C、1或-
| ||||
D、1或
|
函数f(x)=2x-
的零点在区间( )
| 1 |
| x |
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
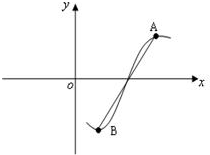 函数f(x)=cos(ωx+φ)(ω>0,0<φ<π)为R上的奇函数,该函数的部分图象如图所表示,A,B分别为最高点与最低点,并且两点间的距离为2
函数f(x)=cos(ωx+φ)(ω>0,0<φ<π)为R上的奇函数,该函数的部分图象如图所表示,A,B分别为最高点与最低点,并且两点间的距离为2