题目内容
18.下列说法正确的是( )| A. | 若l∥α,l∥β,则α∥β | B. | 若l∥α,l⊥β,则α⊥β | C. | 若l⊥α,α⊥β,则l∥β | D. | 若l∥α,α⊥β,则l⊥β |
分析 对4个选项分别进行判断,即可得出结论.
解答 解:对于A,若l∥α,l∥β,则α∥β或α,β相交,不正确;
对于B,若l∥α,经过l的直线与α的交线为m,则l∥m,∵l⊥β,∴m⊥β,根据平面与平面垂直的判定定理,可得α⊥β,正确;
对于C,若l⊥α,α⊥β,则l∥β或l?β,不正确;
对于D,l∥α,α⊥β,则l、β位置关系不确定,不正确,
故选:B.
点评 本题考查空间线面、面面位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
9.函数$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,则f(x)的解析式是( )
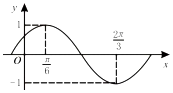

| A. | $f(x)=sin(x+\frac{π}{6})$ | B. | $f(x)=sin(x+\frac{π}{3})$ | C. | $f(x)=sin(2x+\frac{π}{6})$ | D. | $f(x)=sin(2x+\frac{π}{3})$ |
13.设函数的定义域为D,若满足条件:存在[a,b]⊆D,使f(x)在[a,b]上的值域为$[{\frac{a}{2},\frac{b}{2}}]$,则称f(x)为“倍缩函数”.若函数f(x)=ex+t为“倍缩函数”,则实数t的取值范围是( )
| A. | $({-∞,-\frac{1+ln2}{2}}]$ | B. | $({-∞,-\frac{1+ln2}{2}})$ | C. | $[{\frac{1+ln2}{2},+∞})$ | D. | $({\frac{1+ln2}{2},+∞})$ |
7.己知${a^{\frac{2}{3}}}=\frac{4}{9}(a>0)$,则${log_a}\frac{3}{2}$=( )
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | -3 | D. | 3 |
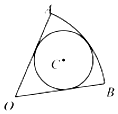 如图,圆C内切于扇形AOB,$∠AOB=\frac{π}{3}$,若在扇形AOB内任取一点,则该点在圆C内的概率为$\frac{2}{3}$.
如图,圆C内切于扇形AOB,$∠AOB=\frac{π}{3}$,若在扇形AOB内任取一点,则该点在圆C内的概率为$\frac{2}{3}$.