题目内容
已知函数f(x)=lnx,g(x)=2-
(a为实数).
(Ⅰ)当a=1时,求函数φ(x)=f(x)-g(x)的最小值;
(Ⅱ)若方程e2f(x)=1.5g(x)(其中e=2.71828…)在区间[0.5,2]上有解,求实数a的取值范围.
(Ⅲ)若u(x)=f(x)+x2+2mx,当y=u(x)存在极值时,求m的取值范围,并证明极值之和小于-3-ln2.
| a |
| x |
(Ⅰ)当a=1时,求函数φ(x)=f(x)-g(x)的最小值;
(Ⅱ)若方程e2f(x)=1.5g(x)(其中e=2.71828…)在区间[0.5,2]上有解,求实数a的取值范围.
(Ⅲ)若u(x)=f(x)+x2+2mx,当y=u(x)存在极值时,求m的取值范围,并证明极值之和小于-3-ln2.
考点:利用导数研究函数的极值,利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:综合题,导数的概念及应用
分析:(Ⅰ)当a=1时,函数φ(x)=f(x)-g(x),求导数,可得函数的单调性,即可求出函数的最小值;
(Ⅱ)方程e2f(x)=1.5g(x)在区间[0.5,2]上有解,可得a=2x-
x3在区间[0.5,2]上有解,求出右边的值域,即可求实数a的取值范围.
(Ⅲ)利用韦达定理,结合根的判别式,即可证明结论.
(Ⅱ)方程e2f(x)=1.5g(x)在区间[0.5,2]上有解,可得a=2x-
| 2 |
| 3 |
(Ⅲ)利用韦达定理,结合根的判别式,即可证明结论.
解答:
(Ⅰ)解:当a=1时,函数φ(x)=f(x)-g(x)=lnx+
-2,
则φ′(x)=
,
∴(0,1)上,φ′(x)<0,(1+∞)上,φ′(x)>0,
∴φ(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
∴φ(x)的最小值为0;
(Ⅱ)解:方程e2f(x)=1.5g(x)在区间[0.5,2]上有解,可得a=2x-
x3在区间[0.5,2]上有解
令h(x)=2x-
x3(x∈[0.5,2]),则h′(x)=2(1-x)(1+x),
∴(0.5,1)上,h′(x)>0,(1,2)上,h′(x)<0,
∴h(x)在(0.5,1)上单调递增,在(1,2)上单调递减,
∵h(0.5)=
,h(1)=
,h(2)=-
,
∴h(x)∈[-
,
],
∴a∈[-
,
];
(Ⅲ)证明:∵u(x)=f(x)+x2+2mx,
∴u′(x)=
,
由-m>0且△>0,可得m<-
,y=u(x)存在极值,
设y=u(x)的极值点为x1,x2,则y=u(x)的极值为u(x1),u(x2),
∴x1+x2=-m,x1x2=
,
∴u(x1)+u(x2)=-ln2-1-m2<-3-ln2.
| 1 |
| x |
则φ′(x)=
| x-1 |
| x2 |
∴(0,1)上,φ′(x)<0,(1+∞)上,φ′(x)>0,
∴φ(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
∴φ(x)的最小值为0;
(Ⅱ)解:方程e2f(x)=1.5g(x)在区间[0.5,2]上有解,可得a=2x-
| 2 |
| 3 |
令h(x)=2x-
| 2 |
| 3 |
∴(0.5,1)上,h′(x)>0,(1,2)上,h′(x)<0,
∴h(x)在(0.5,1)上单调递增,在(1,2)上单调递减,
∵h(0.5)=
| 11 |
| 12 |
| 4 |
| 3 |
| 4 |
| 3 |
∴h(x)∈[-
| 4 |
| 3 |
| 4 |
| 3 |
∴a∈[-
| 4 |
| 3 |
| 4 |
| 3 |
(Ⅲ)证明:∵u(x)=f(x)+x2+2mx,
∴u′(x)=
| 2x2+2mx+1 |
| x |
由-m>0且△>0,可得m<-
| 2 |
设y=u(x)的极值点为x1,x2,则y=u(x)的极值为u(x1),u(x2),
∴x1+x2=-m,x1x2=
| 1 |
| 2 |
∴u(x1)+u(x2)=-ln2-1-m2<-3-ln2.
点评:本题考查利用导数求闭区间上函数的最值,考查函数的单调性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
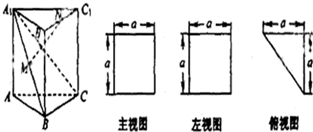 一个多面体的直观图和三视图(主观图、左视图、俯视图)如图所示,M、N分别为A1B、B1C1的中点.
一个多面体的直观图和三视图(主观图、左视图、俯视图)如图所示,M、N分别为A1B、B1C1的中点.