题目内容
14.已知复数z满足z(1+2i)=5i(i为虚数单位).(1)求复数z,以及复数z的实部与虚部;
(2)求复数$\overline{z}$+$\frac{5}{z}$的模.
分析 (1)由z(1+2i)=5i,则$z=\frac{5i}{1+2i}$,利用复数代数形式的乘除运算进行化简,即可求出答案;
(2)由z=2+i,则$\overline{z}=2-i$,把$\overline{z}$代入$\overline{z}$+$\frac{5}{z}$,利用复数代数形式的乘除运算进行化简,再由复数模的公式计算即可.
解答 解:(1)由z(1+2i)=5i,
则z=$\frac{5i}{1+2i}=\frac{5i(1-2i)}{(1+2i)(1-2i)}=2+i$,
∴复数z的实部为:2,虚部为:1;
(2)由z=2+i,则$\overline{z}=2-i$,
∴$\overline{z}$+$\frac{5}{z}$=$2-i+\frac{5}{2+i}=2-i+\frac{5(2-i)}{(2+i)(2-i)}$=2-i+2-i=4-2i.
∴$|\overline{z}+\frac{5}{z}|=\sqrt{{4}^{2}+(-2)^{2}}=2\sqrt{5}$.
即复数$\overline{z}$+$\frac{5}{z}$的模为:$2\sqrt{5}$.
点评 本题考查了复数代数形式的乘除运算,考查了复数模的求法,是基础题.

练习册系列答案
相关题目
5.已知函数y=f(x)的定义域为(0,+∞),当x>1时,f(x)<0,且对任意的x,y∈R,恒有f(xy)=f(x)+f(y),则不等式f(x)+f(x-2)≥f(8)的解集为( )
| A. | (2,4] | B. | [-2,4] | C. | [4,+∞) | D. | (-∞,-2]∪[4,+∞) |
2.二次函数y=(x+2)2-1的图象大致为( )
| A. |  | B. |  | ||
| C. |  | D. |  |
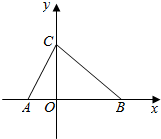 如图,在平面直角坐标系xOy中,∠CAB=60°,AC=4,BC=2$\sqrt{7}$
如图,在平面直角坐标系xOy中,∠CAB=60°,AC=4,BC=2$\sqrt{7}$