题目内容
12. 在长方体ABCD-A1B1C1D1中,E,F分别是AB,CD1的中点,AA1=AD=1,AB=2..
在长方体ABCD-A1B1C1D1中,E,F分别是AB,CD1的中点,AA1=AD=1,AB=2..(1)求证:EF∥平面BCC1B1;
(2))求证:平面CD1E⊥平面D1DE;
(3)求三棱锥F-D1DE的体积.
分析 (1)过F作FM∥C1D1交CC1于M,连结BM,推导出EBMF是平行四边形,从而EF∥BM,由此能证明EF∥平面BCC1B1.
(2)推导出D1D⊥CE,CE⊥DE,从而CE⊥平面D1DE,由此能证明平面CD1E⊥平面D1DE.
(3)由${V}_{F-{D}_{1}DE}={V}_{E-{D}_{1}DF}$,能求出三棱锥F-D1DE的体积.
解答 证明:(1)过F作FM∥C1D1交CC1于M,连结BM,
∵F是CD1的中点,∴FM∥C1D1,FM=$\frac{1}{2}$C1D1,(2分)
又∵E是AB中点,∴BE∥C1D1,BE=$\frac{1}{2}$C1D1,
∴BE∥FM,BE=FM,EBMF是平行四边形,∴EF∥BM
又BM在平面BCC1B1内,∴EF∥平面BCC1B1.(4分)
(2)∵D1D⊥平面ABCD,CE在平面ABCD内,∴D1D⊥CE
在矩形ABCD中,DE2=CE2=2,∴DE2+CE2=4=CD2,(6分)
∴△CED是直角三角形,∴CE⊥DE,∴CE⊥平面D1DE,
∵CE在平面CD1E内,∴平面CD1E⊥平面D1DE.(8分)
解:(3)三棱锥F-D1DE的体积:
${V}_{F-{D}_{1}DE}={V}_{E-{D}_{1}DF}$
=$\frac{1}{3}×{S}_{△{D}_{1}DF}×AD$
=$\frac{1}{3}×\frac{1}{2}×{D}_{1}D×\frac{1}{2}CD×AD$=$\frac{1}{6}$.(12分)
点评 本题考查线面平行的证明,考查面面垂直的证明,考查三棱锥的体积的求不地,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
3.已知函数f(x)=$\left\{\begin{array}{l}{2^x},(x<2)\\ f(x-2),\;\;(x≥2)\end{array}$,则f(5)的值为( )
| A. | $\frac{3}{2}$ | B. | 1 | C. | 2 | D. | 3 |
7.设集合M={x|x2-x-2<0},N={x|x≤k},若M?N,则k的取值范围是( )
| A. | (-∞,2] | B. | [-1,+∞) | C. | (-1,+∞) | D. | [2,+∞) |
17.若x,y满足条件$\left\{\begin{array}{l}x-y+2≥0\\ x+y-4≤0\\ y≥2\end{array}\right.$,则z=2x-y的最小值为( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
4.在自然界中存在着大量的周期函数,比如声波.若两个声波随时间的变化规律分别为:y1=3$\sqrt{2}$sin(100πt),y2=3sin(100πt-$\frac{π}{4}$),则这两个声波合成后(即y=y1+y2)的声波的振幅为( )
| A. | 6$\sqrt{2}$ | B. | 3+3$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 3$\sqrt{5}$ |
2.《九章算术》是我国古代第一部数学专著,全书收集了246个问题及其解法,其中一个问题为“现有一根九节的竹子,自上而下各节的容积成等差数列,上面四节容积之和为3升,下面三节的容积之和为4升,求中间两节的容积各为多少?”该问题中第2节,第3节,第8节竹子的容积之和为( )
| A. | $\frac{17}{6}$升 | B. | $\frac{7}{2}$升 | C. | $\frac{113}{66}$升 | D. | $\frac{109}{33}$升 |
 如图,正方形边长是2,函数y=$\frac{1}{2x}$与正方形交于两点,向正方形内投飞镖,则飞镖落在阴影部分内的概率是$\frac{7-3ln2}{8}$.
如图,正方形边长是2,函数y=$\frac{1}{2x}$与正方形交于两点,向正方形内投飞镖,则飞镖落在阴影部分内的概率是$\frac{7-3ln2}{8}$.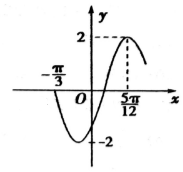 函数f(x)=Asin(ωx+φ),x∈R,(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=Asin(ωx+φ),x∈R,(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示.