题目内容
函数y=(x-1)(x-2)(x-3)(x-4)+15的值域为 .
考点:函数的值域
专题:函数的性质及应用
分析:将函数的表达式转化为y=(x2-5x+5)2+14的形式,从而求出函数的值域问题.
解答:
解:y=(x-1)(x-2)(x-3)(x-4)+15
=[(x-1)(x-4)][(x-2)(x-3)]+15
=(x2-5x+4)(x2-5x+6)+15
=(x2-5x+4)[(x2-5x+4)+2]+15
=(x2-5x+4)2+2(x2-5x+4)+15
=[(x2-5x+4)2+2(x2-5x+4)+1]+14
=(x2-5x+5)2+14
∴y≥14,
故答案为:[14,+∞).
=[(x-1)(x-4)][(x-2)(x-3)]+15
=(x2-5x+4)(x2-5x+6)+15
=(x2-5x+4)[(x2-5x+4)+2]+15
=(x2-5x+4)2+2(x2-5x+4)+15
=[(x2-5x+4)2+2(x2-5x+4)+1]+14
=(x2-5x+5)2+14
∴y≥14,
故答案为:[14,+∞).
点评:本题考查了函数的值域问题,考查了值思想,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知线段PQ=
如图,已知线段PQ=



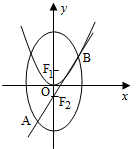 如图所示,椭圆C:
如图所示,椭圆C: