题目内容
设函数f(x)=(1+x)2-2ln(1+x).
(1)求函数f(x)的单调区间;
(2)若关于x的方程f(x)=x2+x+a在[0,2]上恰有两个相异实根,求实数a的取值范围.
(1)求函数f(x)的单调区间;
(2)若关于x的方程f(x)=x2+x+a在[0,2]上恰有两个相异实根,求实数a的取值范围.
考点:利用导数研究函数的单调性,函数的零点与方程根的关系
专题:导数的综合应用
分析:(1)先求出函数的导数,从而求出单调区间,(2)引进新函数g(x)由题意得出方程组,从而求出a的范围.
解答:
解:(1)函数的定义域为(-1,+∞),
∵f(x)=(1+x)2-2ln(1+x),
∴f′(x)=2(x+1-
),
由f′(x)>0,得x>0;
由f′(x)<0,得-1<x<0,
∴f(x)的递增区间是(0,+∞),递减区间是(-1,0).
(2)方程f(x)=x2+x+a,
即x-a+1-2ln(1+x)=0,
记g(x)=x-a+1-2ln(1+x)(x>-1),
则g′(x)=1-
=
,
由g′(x)>0,得x>1;由g′(x)<0,得-1<x<1.
所以g(x)在[0,1]上单调递减,在[1,2]上单调递增.
为使f(x)=x2+x+a在[0,2]上恰有两个相异的实根,
只须g(x)=0在[0,1)和(1,2]上各有一个实根,
于是有
,即
,
解得2-2ln 2<a≤3-2ln 3,
故实数a的取值范围是(2-2ln 2,3-2ln 3].
∵f(x)=(1+x)2-2ln(1+x),
∴f′(x)=2(x+1-
| 1 |
| x+1 |
由f′(x)>0,得x>0;
由f′(x)<0,得-1<x<0,
∴f(x)的递增区间是(0,+∞),递减区间是(-1,0).
(2)方程f(x)=x2+x+a,
即x-a+1-2ln(1+x)=0,
记g(x)=x-a+1-2ln(1+x)(x>-1),
则g′(x)=1-
| 2 |
| 1+x |
| x-1 |
| x+1 |
由g′(x)>0,得x>1;由g′(x)<0,得-1<x<1.
所以g(x)在[0,1]上单调递减,在[1,2]上单调递增.
为使f(x)=x2+x+a在[0,2]上恰有两个相异的实根,
只须g(x)=0在[0,1)和(1,2]上各有一个实根,
于是有
|
|
解得2-2ln 2<a≤3-2ln 3,
故实数a的取值范围是(2-2ln 2,3-2ln 3].
点评:本题考察了函数的单调性,函数的零点与方程的根的关系,导数的应用,是一道综合题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
自然数都是整数,而4是自然数,所以4是整数.以上三段论推理( )
| A、大前提错误 |
| B、推理形式不正确 |
| C、两个“整数”概念不一致 |
| D、正确 |
若将6本不同书放到5个不同盒子里,有多少种不同放法( )
A、
| ||
B、
| ||
| C、56 | ||
| D、65 |
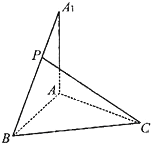 已知AA1⊥平面ABC,AA1=AB=BC=CA=3,P为A1B上的点.
已知AA1⊥平面ABC,AA1=AB=BC=CA=3,P为A1B上的点.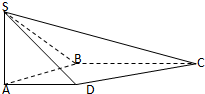 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=1,
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=1,