题目内容
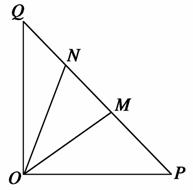
如图,在等腰直角△OPQ中,∠POQ=90°,OP=2 ,点M在线段PQ上.
,点M在线段PQ上.
(1)若OM=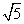 ,求PM的长;
,求PM的长;
(2)若点N在线段MQ上,且∠MON=30°,问:当∠POM取何值时,△OMN的面积最小?并求出面积的最小值.
解 (1)在△OMP中,∠P=45°,OM=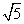 ,OP=2
,OP=2 .
.
由余弦定理得,OM2=OP2+PM2-2×OP×PM×cos45°,
得PM2-4PM+3=0,解得PM=1或PM=3.
(2)设∠POM=α,0°≤α≤60°,
在△OMP中,由正弦定理,得 =
= ,
,
 故S△OMN=
故S△OMN= ×OM×ON×sin∠MON
×OM×ON×sin∠MON

 因为0°≤α≤60°,30°≤2α+30°≤150°,所以当α=30°时,sin(2α+30°)的最大值为1,此时△OMN的面积取到最小值.即∠POM=30°时,△OMN的面积最小,其最小值为8-4
因为0°≤α≤60°,30°≤2α+30°≤150°,所以当α=30°时,sin(2α+30°)的最大值为1,此时△OMN的面积取到最小值.即∠POM=30°时,△OMN的面积最小,其最小值为8-4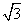 .
.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 A.
A. B.-
B.- D.-
D.-
 ab,则C=( )
ab,则C=( )
 =0,则△ABC的内角A等于( )
=0,则△ABC的内角A等于( )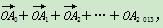 其结果为( )
其结果为( )
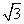 ),C(3,0) ,动点D满足|
),C(3,0) ,动点D满足| |=1,则|
|=1,则| |的最大值是________.
|的最大值是________.