题目内容
10.设$f(x)=\left\{\begin{array}{l}{2^{x-2}},x≤2\\{log_2}^{(x-1)},x>2\end{array}\right.$,则f[f(5)]=( )| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
分析 先求出f(5)=log24=2,从而f[f(5)]=f(2),由此能求出结果.
解答 解:∵$f(x)=\left\{\begin{array}{l}{2^{x-2}},x≤2\\{log_2}^{(x-1)},x>2\end{array}\right.$,
∴f(5)=log24=2,
f[f(5)]=f(2)=22-2=1.
故选:B.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
5.定义域为R的函数f(x)满足f(x+1)=2f(x),且当x∈[0,1]时,f(x)=x2-x,则当x∈[-2,-1]时,f(x)的最小值为( )
| A. | -$\frac{1}{16}$ | B. | -$\frac{1}{8}$ | C. | -$\frac{1}{4}$ | D. | 0 |
15.已知某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{7}{2}$ | B. | $\frac{14}{3}$ | C. | 7 | D. | 14 |
19.正方体ABCD-A1B1C1D1中,与对角线A1B成45°的棱有( )条.
| A. | 4 | B. | 8 | C. | 12 | D. | 2 |
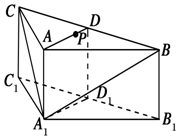 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点.