题目内容
若曲线C1:x2+y2-8x=0与曲线C2:y(y-mx-m)=0有四个不同交点,则实数m的取值范围是( )
A、(-
| ||||
B、(-
| ||||
C、[-
| ||||
D、(-∞,-
|
考点:圆的一般方程
专题:直线与圆
分析:曲线C1表示以C1:(4,0)为圆心、半径等于4的圆;①当m≠0时,曲线C2表示x轴及过点(-1,0)且斜率为m的直线,要使两条曲线有四个不同交点,需y=m(x+1)和圆 (x-4)2+y2=16 相交,根据圆心到此直线的距离小于半径,求得m的范围.②当m=0时,检验不满足条件.综合可得m的范围.
解答:
解:曲线C1:x2+y2-8x=0 即 (x-4)2+y2=16,表示以C1:(4,0)为圆心、半径等于4的圆.
对于曲线C2:y(y-mx-m)=0,①当m≠0时,曲线C2即 y=0,或y=m(x+1),表示x轴及过点(-1,0)且斜率为m的直线,
要使两条曲线有四个不同交点,需y=m(x+1)和圆 (x-4)2+y2=16 相交,
故有
<4,求得-
<m<
,且m≠0.
②当m=0时,曲线C2:即y2=0,即y=0,表示一条直线,此时曲线C2和曲线C1 只有一个交点,不满足条件.
综上可得,实数m的取值范围是(-
,0)∪(0,
),
故选:B.
对于曲线C2:y(y-mx-m)=0,①当m≠0时,曲线C2即 y=0,或y=m(x+1),表示x轴及过点(-1,0)且斜率为m的直线,
要使两条曲线有四个不同交点,需y=m(x+1)和圆 (x-4)2+y2=16 相交,
故有
| |4m-0+m| | ||
|
| 4 |
| 3 |
| 4 |
| 3 |
②当m=0时,曲线C2:即y2=0,即y=0,表示一条直线,此时曲线C2和曲线C1 只有一个交点,不满足条件.
综上可得,实数m的取值范围是(-
| 4 |
| 3 |
| 4 |
| 3 |
故选:B.
点评:本题主要考查曲线的方程,直线和圆的位置关系,点到直线的距离公式,体现了转化的数学思想,属于基础题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
若原点和点(1,1)都在直线x+y=a的同一侧,则a的取值范围是( )
| A、a<0或a>2 |
| B、0<a<2 |
| C、a=0或a=2 |
| D、0≤a≤2 |
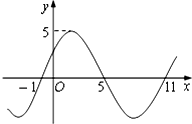 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0≤φ<2π)在R上的部分图象如图所示,则f(2014)=
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0≤φ<2π)在R上的部分图象如图所示,则f(2014)=