题目内容
已知函数y=
与y=
,分别求这两个函数的定义域和值域.
| 2x+1 |
| 1 | |||
|
考点:函数的值域
专题:函数的性质及应用
分析:对于y=
,由2x+1≥0,得x≥-
,从而求出定义域,值域;对于y=
,由2x+1≠0,得x≠-
,从而求出定义域,值域.
| 2x+1 |
| 1 |
| 2 |
| 1 | |||
|
| 1 |
| 2 |
解答:
解:对于y=
,2x+1≥0,x≥-
,
∴定义域为:[-
,+∞),值域为[0,+∞);
对于y=
,2x+1≠0,x≠-
,
∴定义域为:(-∞,-
)∪(-
,+∞),
值域为:(-∞,0)∪(0,+∞).
| 2x+1 |
| 1 |
| 2 |
∴定义域为:[-
| 1 |
| 2 |
对于y=
| 1 | |||
|
| 1 |
| 2 |
∴定义域为:(-∞,-
| 1 |
| 2 |
| 1 |
| 2 |
值域为:(-∞,0)∪(0,+∞).
点评:本题考查了函数的定义域,值域问题,求值域时注意定义域的范围.

练习册系列答案
相关题目
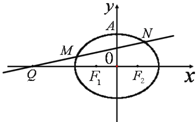 如图,已知椭圆C:
如图,已知椭圆C: