题目内容
6．用反证法证明命题：“三角形的内角中至少有一个不大于60°”时，结论的否定是三角形的三个内角都大于60°．分析 找到“三角形的内角中至少有一个不小于60°”的对立事件，由此能求出结果．
解答 解：根据反证法的步骤，第一步应假设结论的反面成立，即三角形的三个内角都大于60°．
故答案为：三角形的三个内角都大于60°．
点评 本题考查反证法的应用，是基础题，解题时要认真审题，注意反证法性质的合理运用．
练习册系列答案
相关题目
16．若a，b∈R，且ab＞0，则$\frac{b}{a}$+$\frac{a}{b}$的最小值是（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | 2 | D． | 2$\sqrt{2}$ |
17．
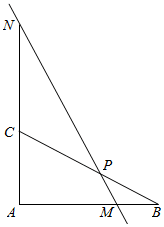如图，Rt△ABC中，P是斜边BC上一点，且满足：$\overrightarrow{BP}=\frac{1}{2}\overrightarrow{PC}$，点M，N在过点P的直线上，若$\overrightarrow{AM}=λ\overrightarrow{AB}，\overrightarrow{AN}=μ\overrightarrow{AC}$，（λ，μ＞0），则λ+2μ的最小值为（ ）
如图，Rt△ABC中，P是斜边BC上一点，且满足：$\overrightarrow{BP}=\frac{1}{2}\overrightarrow{PC}$，点M，N在过点P的直线上，若$\overrightarrow{AM}=λ\overrightarrow{AB}，\overrightarrow{AN}=μ\overrightarrow{AC}$，（λ，μ＞0），则λ+2μ的最小值为（ ）| A． | 2 | B． | $\frac{8}{3}$ | C． | 3 | D． | $\frac{10}{3}$ |
14．
如图，已知点D为△ABC的边BC上一点，$\overrightarrow{BD}$=3$\overrightarrow{DC}$，En（n∈N+）为边AC上的点，满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1，$\overrightarrow{{E}_{n}B}$=（4an+3）$\overrightarrow{{E}_{n}D}$，其中实数列{an}中an＞0，a1=1，则{an}的通项公式为（ ）
如图，已知点D为△ABC的边BC上一点，$\overrightarrow{BD}$=3$\overrightarrow{DC}$，En（n∈N+）为边AC上的点，满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1，$\overrightarrow{{E}_{n}B}$=（4an+3）$\overrightarrow{{E}_{n}D}$，其中实数列{an}中an＞0，a1=1，则{an}的通项公式为（ ）| A． | 3•2n-1-2 | B． | 2n-1 | C． | 4n-2 | D． | 2•4n-1-1 |
1．曲线y=-ln（2x+1）+2在点（0，2）处的切线与直线y=0和y=2x围成的三角形的面积为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | 1 |
15．在下列函数中，最小值为2的是（ ）
| A． | y=2x+2-x | B． | y=sinx+$\frac{1}{sinx}$（0＜x＜$\frac{π}{2}$） | ||
| C． | y=x+$\frac{1}{x}$ | D． | y=log3x+$\frac{1}{lo{g}_{3}x}$（1＜x＜3） |
16．设i是虚数单位，则复数z=$\frac{1+3i}{1-2i}$的共轭复数$\overline{z}$在复平面内对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |