题目内容
16．设i是虚数单位，则复数z=$\frac{1+3i}{1-2i}$的共轭复数$\overline{z}$在复平面内对应的点位于（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 根据复数的四则运算进行化简，结合复数的几何意义即可得到结论．
解答 解：复数z=$\frac{1+3i}{1-2i}$=$\frac{（1+3i）（1+2i）}{（1+2i）（1-2i）}$=$\frac{1-6+3i+2i}{5}$=-1+i，
∴共轭复数$\overline{z}$=-1-i，
∴$\overline{z}$在复平面内对应的点（-1，-1），
故共轭复数$\overline{z}$在复平面内对应的点位于第三象限．
故选：C
点评 本题主要考查复数的几何意义，利用复数的基本运算进行化简是解决本题的关键．
练习册系列答案
互动英语系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
4．已知数列{an}满足：a1=-13，a6+a8=-2，且an-1=2an-an+1（n≥2），则数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前13项和为（ ）
| A． | $\frac{1}{13}$ | B． | -$\frac{1}{13}$ | C． | $\frac{1}{11}$ | D． | -$\frac{1}{11}$ |
8．已知函数$f（x）=kx（x∈[\frac{1}{e}，e]）$，$g（x）={（\frac{1}{e}）^{\frac{x}{2}}}$，若f（x），g（x）图象上分别存在点M，N，使得M，N关于直线y=x对称，则实数k的取值范围为（ ）
| A． | $[-\frac{1}{e}，e]$ | B． | $[-\frac{2}{e}，2e]$ | C． | $[-\frac{3}{e}，3e]$ | D． | $（-\frac{2}{e}，2e）$ |
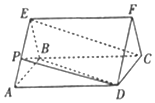如图，三棱柱ABE-DCF中，△EAB是正三角形，四边形ABCD是矩形，且EA=2，BC=2$\sqrt{3}$，EC=4．