题目内容

求函数y=
x2-4x+8
+
x2-16x+80
的最小值．
考点：函数的最值及其几何意义
专题：计算题,函数的性质及应用
分析：y=
x2-4x+8
+
x2-16x+80
=
(x-2)2+(0-2)2
+
(x-4)2+(0-8)2
，表示x轴上的点（x，0）与（2，2），（4，8）两点的距离的和，利用取对称点的方法，即可求出函数y=
x2-4x+8
+
x2-16x+80
的最小值．
解答： 解：y=
x2-4x+8
+
x2-16x+80
=
(x-2)2+(0-2)2
+
(x-4)2+(0-8)2
，
表示x轴上的点（x，0）与（2，2），（4，8）两点的距离的和，
取（2，2）关于x轴的对称点（-2，2），则（-2，2），（4，8）两点的距离的和最小为
(-2-4)2+(2-8)2
=6
2
．
点评：本题考查函数的最值及其几何意义，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=a-
2
2x+1
（a∈R）
（1）判断并证明函数的单调性；
（2）若函数为f（x）奇函数，求实a数的值；
（3）在（2）的条件下，若对任意的t∈R，不等式f（t2+2）+f（-t2-t）＞0恒成立，求实数t的取值范围．
已知数列{an}中，a1=1，Sn=2an-1（Sn为数列{an}的前n项和），数列{bn}为等差数列且满足b1=a4，b4=a2；
（1）求数列{an}的通项公式；
（2）设数列{|bn|}的前n项和为Tn，求Tn．
如图，在四棱锥E-ABCD中，AB⊥平面BCE，DC⊥平面BCE，AB=BC=CE=2CD=2，∠BCE=
2π
3
．
（ I）求证：平面ADE⊥平面ABE；
（Ⅱ）求二面角A-EB-D的大小．
设f（x）=ax2-6lnx，其中a∈R，曲线y=f（x）在点（1，f（1））处的切线与y轴相交于点（0，3）．
（1）确定a的值；
（2）求函数f（x）的单调区间与极值．
若二阶矩阵M满足：M
12
34
=
58
46
．
（Ⅰ）求二阶矩阵M；
（Ⅱ）若曲线C：x2+2xy+2y2=1在矩阵M所对应的变换作用下得到曲线C′，求曲线C′的方程．
设Sn是公差不为0的等差数列{an}的前n项和，已知a1=1，且S1，S2，S4成等比数列；
（1）求数列{an}的通项公式；
（2）求数列{
1
anan+1
}的前n项和．
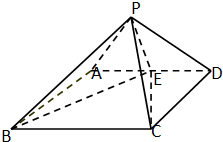如图，四棱锥P-ABCD的底面是矩形，侧面PAD⊥底面ABCD，在△PAD中
PA
+
PD
=2
PE
，且AD=2PE．
（1）求证：平面PAB⊥平面PCD；
（2）如果AB=BC，∠PAD=60°，求DC与平面PBE的正弦值．
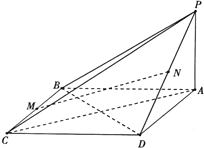在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD为菱形，M，N分别是BC和PD的中点．
（Ⅰ）证明：MN∥平面PAB；
（Ⅱ）证明：平面PBD⊥平面PAC．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网