题目内容
已知定义在R上的函数f(x)满足:f(x)=
且f(x+2)=f(x),g(x)=
,则方程f(x)=g(x)在区间[-5,1]上的所有实根之和为( )
|
| 2x+5 |
| x+2 |
| A、-8 | B、-7 | C、-6 | D、0 |
考点:分段函数的应用
专题:计算题,数形结合,函数的性质及应用
分析:化简g(x)的表达式,得到g(x)的图象关于点(-2,1)对称,由f(x)的周期性,画出f(x),g(x)的图象,通过图象观察[-5,1]上的交点的横坐标的特点,求出它们的和
解答:
 解:由题意知g(x)=
解:由题意知g(x)=
=2+
,函数f(x)的周期为2,
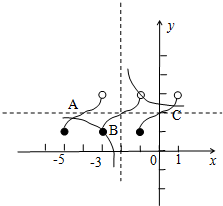
则函数f(x),g(x)在区间[-5,1]上的图象如右图所示:
由图形可知函数f(x),g(x)在区间[-5,1]上的交点为A,B,C,易知点B的横坐标为-3,若设C的横坐标为t
(0<t<1),则点A的横坐标为-4-t,所以方程f(x)=g(x)在区间[-5,1]上的所有实数根之和为-3+(-4-t)+t=-7.
故选:B.
 解:由题意知g(x)=
解:由题意知g(x)=| 2x+5 |
| x+2 |
| 1 |
| x+2 |
则函数f(x),g(x)在区间[-5,1]上的图象如右图所示:
由图形可知函数f(x),g(x)在区间[-5,1]上的交点为A,B,C,易知点B的横坐标为-3,若设C的横坐标为t
(0<t<1),则点A的横坐标为-4-t,所以方程f(x)=g(x)在区间[-5,1]上的所有实数根之和为-3+(-4-t)+t=-7.
故选:B.
点评:本题考查分段函数的图象和运用,考查函数的周期性、对称性和应用,同时考查数形结合的能力,属于中档题.

练习册系列答案
相关题目
在复平面上,复数z=i(1-3i)对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知函数f(x)=x3-3ax(a∈R),若直线x+y+m=0对任意的m∈R都不是曲线y=f(x)的切线,则实数a的取值范围是( )
A、a>
| ||||
B、a<
| ||||
C、a≠
| ||||
D、a<-
|
已知实数x,y满足约束条件
,则z=x+2y的最小值为( )
|
A、
| ||||
| B、11 | ||||
| C、1 | ||||
| D、2 |
下列命题中,是假命题的是( )
A、?x∈(0,
| ||||||||
| B、?x∈R,sinx+cosx≠2 | ||||||||
C、|
| ||||||||
| D、2 2log43=3 |
已知i为虚数单位,若集X={x|x>i2},下列关系式中成立的为( )
| A、0⊆X | B、{0}∈X |
| C、∅∈X | D、{0}⊆X |
函数f(x)=log2x2的图象的大致形状是( )
A、 |
B、 |
C、 |
D、 |
