题目内容
3.定义函数F(a,b)=$\frac{1}{2}$(a+b-|a-b|)(a,b∈R),设函数f(x)=-x2+2x+4,g(x)=x+2(x∈R)函数F(f(x),g(x))的最大值与零点之和为( )| A. | 4 | B. | 6 | C. | $4-2\sqrt{5}$ | D. | $2\sqrt{5}+2$ |
分析 确定函数F(a,b)=$\frac{1}{2}$(a+b-|a-b|)的含义,表示出G(x)=F(f(x),g(x)),根据一次函数与二次函数的性质可求函数的最大值.
解答 解:∵F(a,b)=$\frac{1}{2}$(a+b-|a-b|)=$\left\{\begin{array}{l}{b,a≥b}\\{a,a<b}\end{array}\right.$,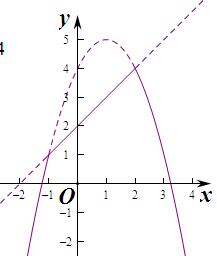
∴设G(x)=F(f(x),g(x))=$\left\{\begin{array}{l}{g(x),f(x)≥g(x)}\\{f(x),f(x)<g(x)}\end{array}\right.$.
∵当-1≤x≤2时,f(x)≥g(x),此时G(x)=x+2∈[1,4],
此时函数无零点,此时最大值为4,
当x>2或x<-1时,f(x)<g(x),G(x)=-x2+2x+4=-(x-1)2+3<4,
综上可得,函数G(x)的最大值为4,
由G(x)=-x2+2x+4=0,得方程的两根之和为2,
则函数F(f(x),g(x))的最大值与零点之和为2+4=6,
故选:B.
点评 本题主要考查分段函数的应用,以及函数的最值的求解,解题的关键是根据题目中的定义求出函数G(x)的解析式.利用数形结合是解决本题的关键.

练习册系列答案
相关题目
14.在三棱锥P-ABC中,已知∠ABC=90°,AB=BC=2,PA⊥平面ABC,且PA=4,则该三棱锥外接球的表面积为( )
| A. | 8π | B. | 24π | C. | 16π | D. | 32π |
11.设变量x,y满足约束条件$\left\{\begin{array}{l}{2x+y≥4}\\{x-y≥1}\\{x-2y≤2}\end{array}\right.$,则x+2y的最小值为( )
| A. | -2 | B. | 1 | C. | 2 | D. | 3 |
8.已知等比数列{an}中,4a1,a3,2a2成等差数列,则公比q=( )
| A. | 2 | B. | -1或-2 | C. | -1或2 | D. | -1 |
15.设等差数列{an}与等比数列{bn}满足:0<a1=b1<a5=b5,则下述结论一定成立的是( )
| A. | a3<b3 | B. | a3>b3 | C. | a6<b6 | D. | a6>b6 |
12.函数f(x)=sin(2x+φ)(|φ|<π)的图象向左平移$\frac{π}{3}$个单位后得到函数g(x)=-cos2x的图象,则函数 f(x)的图象( )
| A. | 关于直线x=$\frac{π}{12}$对称 | B. | 关于直线x=$\frac{5π}{12}$对称 | ||
| C. | 关于点($\frac{π}{12}$,0)对称 | D. | 关于点($\frac{5π}{12}$,0)对称 |
13.函数y=lg(x+1)的定义域是( )
| A. | [-1,+∞) | B. | (-1,+∞) | C. | (0,+∞) | D. | [0,+∞) |
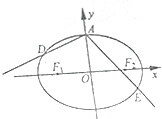 如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,长轴长为2$\sqrt{2}$,左、右焦点分别为F1,F2,上顶点为A.
如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,长轴长为2$\sqrt{2}$,左、右焦点分别为F1,F2,上顶点为A.