题目内容
8.已知sin[(α+β)+α]=5sinβ,求证:2tan(α+β)=3tanα.分析 把已知等式中的角β变为(α+β)-α,2α+β变为(α+β)+α,然后展开两角和与差的正弦得答案.
解答 证明:由5sinβ=sin(2α+β),
得5sin[(α+β)-α]=sin[(α+β)+α],
即5sin(α+β)cosα-5cos(α+β)sinα=sin(α+β)cosα+cos(α+β)sinα,
∴4sin(α+β)cosα=6cos(α+β)sinα,
∵cosα≠0,cos(α+β)≠0,
∴2tan(α+β)=3tanα.
点评 本题考查两角和与差的正弦,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.已知函数f(x)=sinx的图象向右平移m个单位后得到函数g(x)的图象,h(x)=cos(x+$\frac{π}{3}$),g(x)与h(x)图象的零点重合,则m不可能的值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{7π}{6}$ | D. | -$\frac{5π}{6}$ |
3.设正数x,y满足-1<x-y<2,则z=2x-2y的取值范围为( )
| A. | (-∞,4) | B. | (0,4) | C. | ($\frac{1}{4}$,4) | D. | (4,+∞) |
7.已知变量x,y满足约束条件$\left\{\begin{array}{l}x-y+2≤0\\ x≥1\\ x+y-7≤0\end{array}\right.$,则$\frac{x+y}{y}$的取值范围是( )
| A. | $(-∞,\frac{7}{6}]$ | B. | $[\frac{14}{9},+∞)$ | C. | $[\frac{14}{9},7]$ | D. | $[\frac{7}{6},\frac{14}{9}]$ |
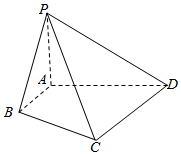 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD中,∠A=90°,AB∥CD,AB=1,AD=CD=2.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD中,∠A=90°,AB∥CD,AB=1,AD=CD=2.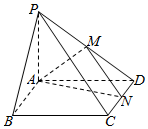 如图在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,PA=AB=2,点M,N分别是PD,DC的中点
如图在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,PA=AB=2,点M,N分别是PD,DC的中点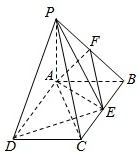 如图PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=2,点F是PB的中点,点E是BC边上的任意一点.
如图PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=2,点F是PB的中点,点E是BC边上的任意一点.