题目内容

已知{an}是公差不为零的等差数列，a1=7，其中a4，a6，a14成等比数列
（1）求{an}的通项；
（2）求|a1|+|a2|+|a3|+…+|an|的值．
考点：数列的求和,等差数列的通项公式
专题：等差数列与等比数列
分析：（1）由已知条件利用等差数列的通项公式和等比数列的性质求出公差，由此能求出{an}的通项．
（2）当n≤3时，an＞0，当n≥4时，an＜0，由此能求出|a1|+|a2|+|a3|+…+|an|的值．
解答： 解：（1）设公差为d（d≠0）
∵a62=a4•a14，
∴(a1+5d)2=(a1+3d)•(a1+13d)，
解得：d=-3，
∴an=-3n+10．
（2）当n≤3时，an＞0，
当n≥4时，an＜0，
令Tn=|a1|+|a2|+|a3|+…+|an|
当n≤3时，Tn=
n(17-3n)
2

当n≥4时，Tn=a1+a2+a3-a4-…-an=12-
(n-3)(-2-3n+10)
2
=
3n2-17n
2
+24，
∴Tn=
n(17-3n)
2
，n≤3
3n2-17n
2
+24，n≥4
．
点评：本题考查数列的通项公式的求法，考查等差数列的各项的绝对值的和的求法，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
相关题目
已知函数f（x）=asinx+bcosx，a≠0，x∈R，f（x）的最大值是2，且在x=
π
6
处的切线方程与直线x-y=0平行．
（1）求a、b的值；
（2）先将f（x）的图象上每点的横坐标缩小为原来的
1
2
，纵坐标不变，再将其向右平移
π
6
个单位得到函数g（x）的图象，已知g（a+
π
4
）=
13
10
，a∈（
π
6
，
π
2
），求cos2a的值．
已知椭圆C1：
x2
a2
+
y2
b2
=1（a＞b＞0）与圆C2：x2+y2=b2，若在椭圆C1上不存在点P，使得由点P所作的圆C2的两条切线互相垂直，则椭圆C1的离心率的取值范围是（　　）
A、（0，
2
2
）
B、（0，
3
2
）
C、[
2
2
，1）
D、[
3
2
，1）
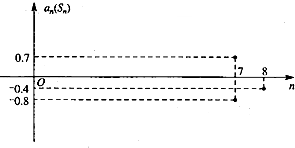设等差数列{an}的前n项和为Sn，在同一个坐标系中，an=f（n）及Sn=g（n）的部分图象如图所示，则（　　）
A、当n=4时，Sn取得最大值
B、当n=3时，Sn取得最大值
C、当n=4时，Sn取得最小值
D、当n=3时，Sn取得最大值
已知数列{an}是等差数列，其前n项和为Sn，a3=6，S3=12．
（1）求数列{an}的通项公式；
（2）求前n项和Sn；
（3）求证：
1
S1
+
1
S2
+…+
1
Sn
＜1．
设数列{an}满足a1=2，an+1-an=3×22n-1，数列{bn}满足bn=log2an
（1）求数列{an}的通项公式；
（2）记数列{
1
bnbn+1
}的前n项和为Tn，若t≥Tn对任意的n∈N+恒成立，求t的取值范围．
设y1=0.3 
1
3
，y2=0.4 
1
3
，y3=0.4 
1
4
（　　）
A、y3＜y2＜y1
B、y1＜y2＜y3
C、y2＜y3＜y1
D、y1＜y3＜y2
已知向量
a
，
b
的模均为2，且＜
a
，
b
＞=
2π
3
，若向量
c
满足|
c
-（
a
+
b
）|=
2
，则|
c
|的取值范围为（　　）
A、[2-
2
，4]
B、[0，2+
2
]
C、[2-
2
，2+
2
]
D、[0，4]
若x∈[0，2]时，函数f（x）=x2+4（log2a-1）x-3在x=2时取得最小值，则a的取值范围为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网