题目内容
15.点$M({x_0},\frac{3}{2})$是抛物线x2=2py(p>0)上一点,若点M到该抛物线焦点的距离为2,则点M到坐标原点的距离为$\frac{\sqrt{21}}{2}$.分析 先根据抛物线的方程求得准线的方程,利用点M到该抛物线的焦点的距离为2,根据抛物线的定义求得P,可得M的坐标,即可得到所求.
解答 解:依题意可知抛物线的准线方程为y=-$\frac{p}{2}$
∵点M(x0,$\frac{3}{2}$)是抛物线x2=2Py(P>0)上一点,点M到该抛物线的焦点的距离为2,
$\frac{p}{2}+\frac{3}{2}=2$,解得P=1.∴抛物线方程为x2=2y,
y=$\frac{3}{2}$时,x0=±$\sqrt{3}$,∴点M到坐标原点的距离为$\sqrt{3+\frac{9}{4}}=\frac{\sqrt{21}}{2}$.
故答案为:$\frac{\sqrt{21}}{2}$
点评 本题主要考查了抛物线的定义的运用.考查了学生对抛物线基础知识的掌握.属中档题.

练习册系列答案
相关题目
10.(理)已知是虚数单位,若$\frac{3+ai}{1-i}$是纯序数,则实数a的值为( )
| A. | 3 | B. | -3 | C. | 2 | D. | -2 |
20.(文)某学校高一、高二、高三年级的学生人数之比为3:3:m,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,若从高三年级抽取的学生人数为20,则实数m=( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
4.已知α为锐角,且sinα=$\frac{4}{5}$,则cos(π+α)=( )
| A. | 一$\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
18.已知函数f(x)=log2(x2-2x-3),则下列各区间中,能满足f(x)单调递减的是( )
| A. | (3,6) | B. | (1,2) | C. | (-1,3) | D. | (-∞,-1) |
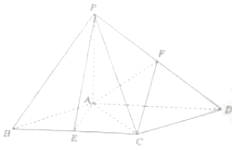 已知四棱锥P-ABCD的底面ABCD为菱形,且PA⊥底面ABCD,∠ABC=60°,点E、F分别为BC、PD的中点,PA=AB=2.
已知四棱锥P-ABCD的底面ABCD为菱形,且PA⊥底面ABCD,∠ABC=60°,点E、F分别为BC、PD的中点,PA=AB=2.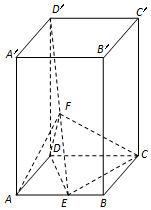 如图,底面为平行四边形的四棱柱ABCD-A'B'C'D'中,DD'⊥平面ABCD,∠DAB=$\frac{π}{3}$,AB=2AD,DD'=3AD,E、F分别是线段AB、D'E的中点.
如图,底面为平行四边形的四棱柱ABCD-A'B'C'D'中,DD'⊥平面ABCD,∠DAB=$\frac{π}{3}$,AB=2AD,DD'=3AD,E、F分别是线段AB、D'E的中点.