题目内容
已知直线l:ax+y=1在矩阵A=
对应的变换作用下变为直线l′:x+by=1.
(1)求实数a,b的值;
(2)求矩阵A的特征值与特征向量.
|
(1)求实数a,b的值;
(2)求矩阵A的特征值与特征向量.
考点:矩阵特征值的定义,特征向量的定义
专题:选作题,矩阵和变换
分析:(1)任取直线l:ax+y=1上一点M(x,y),经矩阵A变换后点为M′(x′,y′),利用矩阵乘法得出坐标之间的关系,求出直线l′的方程,从而建立关于a,b的方程,即可求得实数a,b的值;
(2)先根据特征方程,求出特征值,然后把特征值代入Aα=λα,从而求出特征向量.
(2)先根据特征方程,求出特征值,然后把特征值代入Aα=λα,从而求出特征向量.
解答:
解:(1)设直线l:ax+y=1上任意点M(x,y)在矩阵A对应的变换作用下的像是M′(x′,y′).
由
=
,得
又点M′(x′,y′)在l′上,所以x′+by′=1
即x+(b+2)y=1.
依题意,得
解得a=1,b=-1;
(2)f(λ)=(λ-1)2,得矩阵A特征值为λ1=λ2=1,
将λ1=λ2=1代入方程Aα=λα可解得矩阵A属于特征值λ1=λ2=1的特征向量为
.
由
|
|
|
|
又点M′(x′,y′)在l′上,所以x′+by′=1
即x+(b+2)y=1.
依题意,得
|
解得a=1,b=-1;
(2)f(λ)=(λ-1)2,得矩阵A特征值为λ1=λ2=1,
将λ1=λ2=1代入方程Aα=λα可解得矩阵A属于特征值λ1=λ2=1的特征向量为
|
点评:本题以矩阵为依托,考查矩阵的乘法,考查考查特征值与特征向量,关键是正确利用矩阵的乘法公式.

练习册系列答案
相关题目

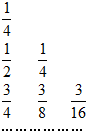 下表给出一个“三角形数阵”(如图),已知每一列的数成等差数列,从第三行起每一行的公比都相等,记第i行第j列的数为aij(i≥j,i,j∈N*).
下表给出一个“三角形数阵”(如图),已知每一列的数成等差数列,从第三行起每一行的公比都相等,记第i行第j列的数为aij(i≥j,i,j∈N*).