Question

已知定义在x∈[-

π

6

，

π

2

]上的函数f（x）=2sin（π-x）cosx．
（Ⅰ）求f（x）的单调递增区间；
（Ⅱ）若方程f（x）=a只有一解，求实数a的取值范围．

Answer 1

考点：函数的零点,正弦函数的单调性

专题：计算题,作图题,函数的性质及应用

分析：（Ⅰ） 化简f（x）=sin2x，其递增区间满足-

π

2

+2kπ≤2x≤

π

2

+2kπ，k∈Z，再由x∈[-

π

6

，

π

2

]解得；
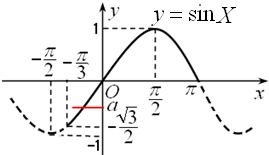
（Ⅱ）在同一坐标系中作出y=sinX=sin2x与y=a的图象，从而解得．

解答： 解：（Ⅰ） 化简得f（x）=sin2x，
其递增区间满足-

π

2

+2kπ≤2x≤

π

2

+2kπ，k∈Z，
再由x∈[-

π

6

，

π

2

]得，
-

π

3

≤2x≤

π

2

⇒-

π

6

≤x≤

π

4

；        
 故所求递增区间为[-

π

6

， 

π

4

]；
（Ⅱ）在同一坐标系中作出y=sinX=sin2x与y=a的图象，
方程只有一解等价于两函数图象只能有一个交点，
所以a的取值范围是：a∈[-

3

2

，  0)∪{ 1 }．

点评：本题考查了函数的图象与性质应用，属于基础题．