题目内容
（Ⅰ）求证：当a＞2时，
+
＜2
；
（Ⅱ）证明：2，
，5不可能是同一个等差数列中的三项．
| a+2 |
| a-2 |
| a |
（Ⅱ）证明：2，
| 3 |
考点：反证法与放缩法
专题：选作题,不等式
分析：（Ⅰ）利用综合法证明即可；
（Ⅱ）利用反证法证明，假设2，
，5是同一个等差数列中的三项，分别设为am，an，ap，推出d=
=
为无理数，又d=
=
=
为有理数，矛盾，即可证明不可能是等差数列中的三项．
（Ⅱ）利用反证法证明，假设2，
| 3 |
| am-an |
| m-n |
2-
| ||
| m-n |
| am-ap |
| m-p |
| 2-5 |
| m-p |
| -3 |
| m-p |
解答：
解：（Ⅰ）∵（
+
）2=2a+2
•
，
＞0，
＞0且a+2≠a-2，
∴2a+
+
＜2a+(a+2)+(a-2)=4a，
∴
+
＜2
----------（7分）
（Ⅱ）假设2，
，5是同一个等差数列中的三项，分别设为am，an，ap，
则d=
=
为无理数，又d=
=
=
为有理数，矛盾．
所以，假设不成立，即2，
，5不可能是同一个等差数列中的三项．-------（14分）
| a+2 |
| a-2 |
| a+2 |
| a-2 |
| a+2 |
| a-2 |
∴2a+
| a+2 |
| a-2 |
∴
| a+2 |
| a-2 |
| a |
（Ⅱ）假设2，
| 3 |
则d=
| am-an |
| m-n |
2-
| ||
| m-n |
| am-ap |
| m-p |
| 2-5 |
| m-p |
| -3 |
| m-p |
所以，假设不成立，即2，
| 3 |
点评：反证法是属于“间接证明法”一类，是从反面的角度思考问题的证明方法，即：肯定题设而否定结论，从而导出矛盾推理而得．应用反证法证明的具体步骤是：①反设：作出与求证结论相反的假设； ②归谬：将反设作为条件，并由此通过一系列的正确推理导出矛盾；③结论：说明反设成立，从而肯定原命题成立．
练习册系列答案
口算题天天练系列答案
相关题目
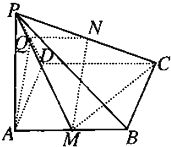已知PA⊥平面ABCD，四边形ABCD为矩形，PA=AD，M、N分别是AB、PC的中点，求证：
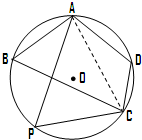市某棚户区改造建筑用地平面示意图如图所示．经规划调研确定，棚改规划建筑用地区域是半径为R的圆面．该圆面的内接四边形ABCD是原棚户建筑用地，测量可知边界AB=AD=4万米，BC=6万米，CD=2万米．