若$tan＜0$.则下列结论正确的是( )A．sinα＞0B．cosα＞0C．sin2α＜0D．cos2α＜0 题目和参考答案——青夏教育精英家教网—

题目内容

15．若$tan（{α+\frac{π}{4}}）＜0$，则下列结论正确的是（　　）

A．

sinα＞0

B．

cosα＞0

C．

sin2α＜0

D．

cos2α＜0

分析先求得α的范围，可得2α的范围，再根据三角函数在各个象限中的符号，得出结论．

解答解：$tan（{α+\frac{π}{4}}）＜0$，等价于kπ-$\frac{π}{2}$＜α+$\frac{π}{4}$＜kπ，等价于kπ-$\frac{3π}{4}$＜α＜kπ-$\frac{π}{4}$，
等价于$2kπ-\frac{3π}{2}＜2α＜2kπ-\frac{π}{2}$，∴cos2α＜0，
故选：D．

点评本题主要考查三角函数在各个象限中的符号，属于基础题．

练习册系列答案

6．（1）已知双曲线E过点P（-2，4$\sqrt{3}$），且与双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{8}$=1有相同的渐近线，求双曲线E的标准方程；
（2）设直线y=kx-1与双曲线E交于A，B两点，则是否存在实数k，使得线段AO和BO垂直，（O为坐标原点），若存在，试求出k的值，若不存在，试说明理由．

3．已知函数f（x）=2$\sqrt{3}$sin（ax-$\frac{π}{4}$）cos（ax-$\frac{π}{4}$）+2cos²（ax-$\frac{π}{4}$）（a＞0），且函数的最小正周期为$\frac{π}{2}$．
（Ⅰ）求a的值；
（Ⅱ）求f（x）在[0，$\frac{π}{4}$]上的最大值和最小值．

10．已知等比数列{a_n}的公比q=2，a₄=8，S_n为{a_n}的前n项和，设a=a₂^0.3，b=0.3${\;}^{{a}_{3}}$，c=log_{a_n}（S_n+$\frac{1}{{S}_{n}}$），则a，b，c大小关系是（　　）

20．函数y=xcosx-sinx的部分图象大致为（　　）

	A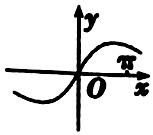．			B．
	C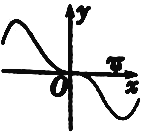．			D．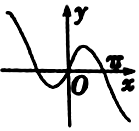

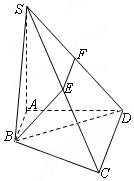7．已知奇函数f（x）=$\left\{\begin{array}{l}{\frac{{e}^{x}}{x}-1（x＞0）}\\{h（x）（x＜0）}\end{array}\right.$，则函数h（x）的最大值为1-e．

4．已知函数f（x）=（x²-x-1）e^x．
（1）求函数f（x）的单调区间．
（2）若方程a（$\frac{f（x）}{{e}^{x}}$+1）+ex=e^x在（0，1）内有解，求实数a的取值范围．

5．

如图，四边形ABCD是梯形，AB∥CD，AB⊥AD，SA⊥平面ABCD，E、F分别是SC、SD的中点，SA=AD=2CD=4AB=4．
（1）求证：EF∥平面SAB；
（2）求证：BE⊥平面SCD；
（3）求二面角B-SD-C的余弦值．

试题分类