题目内容
4.已知函数f(x)=(x2-x-1)ex.(1)求函数f(x)的单调区间.
(2)若方程a($\frac{f(x)}{{e}^{x}}$+1)+ex=ex在(0,1)内有解,求实数a的取值范围.
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)问题可化为ex-ax2+(a-e)x=0,令g(x)=ex-ax2+(a-e)x,则g(x)在(0,1)内有零点,通过讨论a的范围,求出函数的单调区间,从而确定a的范围即可.
解答 解:(1)f′(x)=(x2+x-2)ex=(x-1)(x+2)ex,
令f′(x)>0,解得:x>1或x<-2,
令f′(x)<0,解得:-2<x<1,
故f(x)在(-∞,-2)递增,在(-2,1)递减,在(1,+∞)递增;
(2)方程a($\frac{f(x)}{{e}^{x}}$+1)+ex=ex可化为ex-ax2+(a-e)x=0,
令g(x)=ex-ax2+(a-e)x,则g(x)在(0,1)内有零点,易知g(0)=1,g(1)=0,
g′(x)=ex-2ax+a-e,设g′(x)=h(x),则h′(x)=ex-2a,
①a<0时,h′(x)>0,即h(x)在区间(0,1)递增,h(0)=1+a-e<0,
h(1)=-a>0,即h(x)在区间(0,1)只有1个零点x1,
故g(x)在(0,x1)递减,在(x1,1)递增,
而g(0)=1>0,g(1)=0,得g(x1)<g(1)=0,故g(x)在(0,x1)内存在唯一零点;
②当0≤a≤$\frac{1}{2}$时,h′(x)>0,即h(x)在区间(0,1)递增,
h(x)<h(1)=-a≤0,得g(x)在(0,1)递减,得g(x)在(0,1)无零点;
③当$\frac{1}{2}$<a<$\frac{e}{2}$时,令h′(x)=0,得x=ln(2a)∈(0,1),
∴h(x)在区间(0,ln(2a))上递减,在(ln(2a),1)递增,
h(x)在区间(0,1)上存在最小值h(ln(2a)),
故h(ln(2a))<h(1)=-a<0,h(0)=1+a-e<a-$\frac{e}{2}$<0,
故$\frac{1}{2}$<a<$\frac{e}{2}$时,?x∈(0,1),都有g′(x)<0,g(x)在(0,1)递减,
又g(0)=1,g(1)=0,故g(x)在(0,1)内无零点;
④a≥$\frac{e}{2}$时,h′(x)<0,h(x)在区间(0,1)递减,h(1)=-a<0,h(0)=1+a-e,
若h(0)=1+a-e>0,得a>e-1>$\frac{e}{2}$,
则h(x)在区间(0,1)只有1个零点x2,
故g(x)在(0,x2)递增,在(x2,1)递减,
而g(0)=1,g(1)=0,得g(x)在(0,1)无零点,
若$\frac{e}{2}$<a时,则h(0)=1+a-e<0,得g(x)在(0,1)递减,得g(x)在(0,1)内无零点,
综上,a<0时,方程a($\frac{f(x)}{{e}^{x}}$+1)+ex=ex在(0,1)内有解.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想、考查转化思想,是一道综合题.

| A. | sinα>0 | B. | cosα>0 | C. | sin2α<0 | D. | cos2α<0 |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
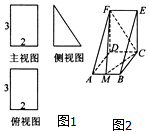 一个多面体的直观图和三视图如图所示,M是AB的 中点,一只蜜蜂在该几何体内自由飞舞,则它飞入几 何体F-AMCD内的概率为( )
一个多面体的直观图和三视图如图所示,M是AB的 中点,一只蜜蜂在该几何体内自由飞舞,则它飞入几 何体F-AMCD内的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
| A. | (-2,1) | B. | (-1,2) | C. | (-∞,0) | D. | (-∞,-2)∪(1,+∞) |
| A. | 数据5,4,4,3,5,2的众数是4 | |
| B. | 若随机变量X~N(3,1)则P(X<4)=p,则(2<X<4)=1-2p | |
| C. | 数据2,3,4,5的标准差是数据4,6,8,10的标准差的一半 | |
| D. | 频率分布直方图中各小长方形的面积等于相应各组的频数 |