题目内容
如图1,△ABC中,∠B=90°,AB=
,BC=1,D、E两点分别是线段AB、AC的中点,现将△ABC沿DE折成直二面角A-DE-B.

(Ⅰ)求证:面ADC⊥面ABE;
(Ⅱ)求直线AD与平面ABE所成角的正切值.
| 2 |

(Ⅰ)求证:面ADC⊥面ABE;
(Ⅱ)求直线AD与平面ABE所成角的正切值.
考点:直线与平面所成的角,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由已知条件推导出∠ADB为二面角A-DE-B平面角,AD⊥面BCD,从而AD⊥BE,由此能证明BE⊥面ADC,从而得到面ABE⊥面ADC.
(Ⅱ)连结BE交CD于H,连结AH,过点D作DO⊥AH于O.由已知条件推导出∠DAO为AD与平面ABE所成角.由此能求出直线AD与平面ABE所成角的正切值.
(Ⅱ)连结BE交CD于H,连结AH,过点D作DO⊥AH于O.由已知条件推导出∠DAO为AD与平面ABE所成角.由此能求出直线AD与平面ABE所成角的正切值.
解答:
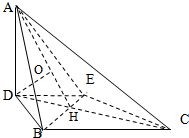 解:(Ⅰ)由∠B=90°,D、E两点分别是线段AB、AC的中点,
解:(Ⅰ)由∠B=90°,D、E两点分别是线段AB、AC的中点,
得DE∥BC,DE⊥AD,DE⊥BD,
∴∠ADB为二面角A-DE-B平面角,∠ADB=
.
∴AD⊥面BCD,又∵BE?面BCD,∴AD⊥BE,
又BD=
,DE=
,BC=1,即
=
,
∴△BDE~△DBC,∴∠EBD=∠DCB,
∴BE⊥DC,∴BE⊥面ADC,
又BE?面ABE,∴面ABE⊥面ADC.
(Ⅱ)连结BE交CD于H,连结AH,
过点D作DO⊥AH于O.
∵AD⊥BE,BE⊥DH,
∴BE⊥面ADHDO?面ADH,∴BE⊥DO,
又DO⊥AH,∴DO⊥面ABE,
∴∠DAO为AD与平面ABE所成角.
Rt△BDE中,BD=
,DE=
∴DH=
=
,
Rt△ADH中,tan∠DAO=
=
×
=
.
∴直线AD与平面ABE所成角的正切值为
.
 解:(Ⅰ)由∠B=90°,D、E两点分别是线段AB、AC的中点,
解:(Ⅰ)由∠B=90°,D、E两点分别是线段AB、AC的中点,得DE∥BC,DE⊥AD,DE⊥BD,
∴∠ADB为二面角A-DE-B平面角,∠ADB=
| π |
| 2 |
∴AD⊥面BCD,又∵BE?面BCD,∴AD⊥BE,
又BD=
| ||
| 2 |
| 1 |
| 2 |
| BD |
| DE |
| BC |
| BD |
∴△BDE~△DBC,∴∠EBD=∠DCB,
∴BE⊥DC,∴BE⊥面ADC,
又BE?面ABE,∴面ABE⊥面ADC.
(Ⅱ)连结BE交CD于H,连结AH,
过点D作DO⊥AH于O.
∵AD⊥BE,BE⊥DH,
∴BE⊥面ADHDO?面ADH,∴BE⊥DO,
又DO⊥AH,∴DO⊥面ABE,
∴∠DAO为AD与平面ABE所成角.
Rt△BDE中,BD=
| ||
| 2 |
| 1 |
| 2 |
| BD•DE |
| BE |
| ||
| 6 |
Rt△ADH中,tan∠DAO=
| DH |
| DA |
| ||
| 6 |
| 2 |
| ||
| 3 |
∴直线AD与平面ABE所成角的正切值为
| ||
| 3 |
点评:本题考查平面与平面垂直的证明,考查直线与平面所成角的正切值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
已知函数f(x)=(
)x-cosx,则f(x)在[0,2π]上的零点个数( )
| 1 |
| 4 |
| A、.1 | B、.2 | C、.3 | D、.4 |