题目内容
已知函数f(x)=x2-2ax+b2,a∈R,b∈R.
(Ⅰ)若a从集合{0,1,2,3,4}中任取一个元素,b从集合{0,1,2,3}中任取一个元素,求方程f(x)=0有两个不相等实根的概率;
(Ⅱ)若a从区间[0,3]中任取一个数,b从区间[0,4]中任取一个数,求方程f(x)=0没有实根的概率.
(Ⅰ)若a从集合{0,1,2,3,4}中任取一个元素,b从集合{0,1,2,3}中任取一个元素,求方程f(x)=0有两个不相等实根的概率;
(Ⅱ)若a从区间[0,3]中任取一个数,b从区间[0,4]中任取一个数,求方程f(x)=0没有实根的概率.
考点:古典概型及其概率计算公式,二次函数的性质
专题:概率与统计
分析:(Ⅰ)由题设a有5种可能情况,b有4种可能情况,一共有4×5=20种情况,由于方程有两不等实数根,a>b有10种情况,由此能求出方程f(x)=0有两个不相等实根的概率.
(Ⅱ)利用几何概型概率计算公式求解.
(Ⅱ)利用几何概型概率计算公式求解.
解答:
解:(Ⅰ)由题设有a有5种可能情况,
b有4种可能情况,一共有4×5=20种情况,
由于方程有两不等实数根,
则a、b满足△=4a2-4b2>0,
即a>b有10种情况,
∴方程f(x)=0有两个不相等实根的概率;
p=
=
(Ⅱ)a从区间[0,3]中任取一个数,
b从区间[0,4]中任取一个数,
方程f(x)=0没有实根的概率:
p=
=
.
b有4种可能情况,一共有4×5=20种情况,
由于方程有两不等实数根,
则a、b满足△=4a2-4b2>0,
即a>b有10种情况,
∴方程f(x)=0有两个不相等实根的概率;
p=
| 10 |
| 20 |
| 1 |
| 2 |
(Ⅱ)a从区间[0,3]中任取一个数,
b从区间[0,4]中任取一个数,
方程f(x)=0没有实根的概率:
p=
12-
| ||
| 12 |
| 5 |
| 8 |
点评:本题考查概率的求法,是中档题,解题时要认真审题,注意几何概型概率计算公式的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若曲线C:
+x2=1和直线l:y=kx+3只有一个公共点,那么k的值为 ( )
| y2 |
| 4 |
A、
| ||||
B、
| ||||
| C、5或-5 | ||||
D、
|
 已知四边形ABCD是菱形,DA=DB=2,DD1⊥面ABCD,点P为线段OD1上的任一点.
已知四边形ABCD是菱形,DA=DB=2,DD1⊥面ABCD,点P为线段OD1上的任一点. 抛物线E:y2=4x的焦点为F,准线l与x轴的交点为A.点C在抛物线E上,以为圆心,|CO|为半径作圆.
抛物线E:y2=4x的焦点为F,准线l与x轴的交点为A.点C在抛物线E上,以为圆心,|CO|为半径作圆.

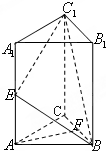 如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=4,E、F分别为AA1、BC的中点.
如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=4,E、F分别为AA1、BC的中点.