题目内容
已知菱形ABCD的边长是2,B=60°,以AC为棱折成一个二面角B-AC-D,使B,D两点的距离是3,则二面角B-AC-D的大小是 .
考点:与二面角有关的立体几何综合题
专题:空间角
分析:连结AC、BD,交于点O,∠BOD是二面角B-AC-D的平面角,利用余弦定理能求出二面角B-AC-D的大小.
解答:
解: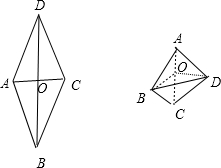 如图,连结AC、BD,交于点O,
如图,连结AC、BD,交于点O,
∵菱形ABCD的边长是2,B=60°,
∴AC⊥DB,DO=AO=
=
,
以AC为棱折成一个二面角B-AC-D,使B,D两点的距离是3,
∵DO⊥AB,BO⊥AB,
∴∠BOD是二面角B-AC-D的平面角,
∵DO=AO=
,BD=3,
∴cos∠BOD=
=-
,
∴∠BOD=120°,
∴二面角B-AC-D的大小为120°.
故答案为:120°.
 如图,连结AC、BD,交于点O,
如图,连结AC、BD,交于点O,∵菱形ABCD的边长是2,B=60°,
∴AC⊥DB,DO=AO=
| 22-12 |
| 3 |
以AC为棱折成一个二面角B-AC-D,使B,D两点的距离是3,
∵DO⊥AB,BO⊥AB,
∴∠BOD是二面角B-AC-D的平面角,
∵DO=AO=
| 3 |
∴cos∠BOD=
(
| ||||
2×
|
| 1 |
| 2 |
∴∠BOD=120°,
∴二面角B-AC-D的大小为120°.
故答案为:120°.
点评:本题考查二面角的大小的求法,是中档题,解题时要认真审题,注意合理地化空间问题为平面问题,注意余弦定理的合理运用.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
若关于x的方程|2x-1|=m有两个不相等的实数根x1和x2,则有( )
| A、x1+x2>0 |
| B、x1+x2≥0 |
| C、x1+x2≤0 |
| D、x1+x2<0 |
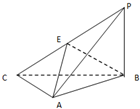 如图,三棱锥P-ABC中,PA⊥平面ABC,PB=BC=CA=4,∠BCA=90°,E为PC中点.
如图,三棱锥P-ABC中,PA⊥平面ABC,PB=BC=CA=4,∠BCA=90°,E为PC中点.