题目内容
若关于x的方程|2x-1|=m有两个不相等的实数根x1和x2，则有（ ）
| A、x1+x2＞0 |
| B、x1+x2≥0 |
| C、x1+x2≤0 |
| D、x1+x2＜0 |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：由题意可得函数y=|2x-1|的图象和直线 y=m有2个交点，设这两个交点的横坐标分别为x1和x2，则0＜m＜1，且x1＜0＜x2，根据1-2x1=2x2-1∈（0，1），可得2x1+2x2=2＞2
，即2x1+x2＜1，由此可得结论．
| 2x1+x2 |
解答：
解：∵关于x的方程|2x-1|=m有两个不相等的实数根x1和x2，
故函数y=|2x-1|的图象和直线 y=m有2个交点，且这两个交点的横坐标分别为x1和x2，0＜m＜1．
不妨设x1＜x2，则设x1＜0＜x2，1-2x1=2x2-1∈（0，1），
∴2x1+2x2=2＞2
，
∴2x1+x2＜1=20，∴x1+x2＜0，
故选：D．
故函数y=|2x-1|的图象和直线 y=m有2个交点，且这两个交点的横坐标分别为x1和x2，0＜m＜1．
不妨设x1＜x2，则设x1＜0＜x2，1-2x1=2x2-1∈（0，1），
∴2x1+2x2=2＞2
| 2x1+x2 |
∴2x1+x2＜1=20，∴x1+x2＜0，
故选：D．
点评：本题主要考查函数的零点与方程的根的关系，基本不等式的应用，属于基础题．
练习册系列答案
相关题目
如图是一个体积为10的空间几何体的三视图，则图中x的值为（ ）
| A、2 | B、3 | C、4 | D、5 |
已知i是虚数单位，则
等于（ ）
| 3-i |
| 2+i |
| A、-1+i | B、-1-i |
| C、1+i | D、1-i |
设Sn为等差数列{an}的前n项和．若a4＜0，a5＞|a4|，则使Sn＞0成立的最小正整数n为（ ）
| A、6 | B、7 | C、8 | D、9 |
若函数f(x)=x+
(b∈R)的导函数在区间（1，2）上有零点，则f（x）在下列区间单调递增的是（ ）
| b |
| x |
| A、（-2，0） |
| B、（0，1） |
| C、（1，+∞） |
| D、（-∞，-2） |
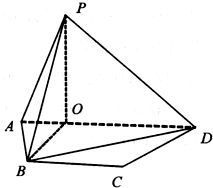如图，等腰梯形ABCD中，AD∥BC，P是平面ABCD外一点，P在平面ABCD的射影O恰在AD上，PA=AB=BC=2AO=2，BO=