题目内容
(本题满分14分) 本题共有3个小题,第1小题4分,第2小题5分,第3小题5分.
设等比数列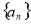 的前
的前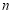 项的和为
项的和为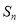 ,公比为
,公比为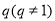 .
.
(1)若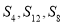 成等差数列,求证:
成等差数列,求证: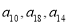 成等差数列;
成等差数列;
(2)若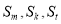 (
(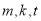 为互不相等的正整数)成等差数列,试问数列
为互不相等的正整数)成等差数列,试问数列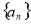 中是否存在不同的三项成等差数列?若存在,写出两组这三项;若不存在,请说明理由;
中是否存在不同的三项成等差数列?若存在,写出两组这三项;若不存在,请说明理由;
(3)若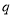 为大于
为大于 的正整数.试问
的正整数.试问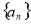 中是否存在一项
中是否存在一项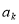 ,使得
,使得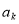 恰好可以表示为该数列中连续两项的和?请说明理由.
恰好可以表示为该数列中连续两项的和?请说明理由.
练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目


 的准线方程是 ( )
的准线方程是 ( ) B.
B. C.
C. D.
D.
 和偶函数
和偶函数 满足
满足
 ,若
,若 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.

 ②
②
 ③
③
 其中能作为表示它们所在平面内所有向量的基底的是 ( )
其中能作为表示它们所在平面内所有向量的基底的是 ( )  .
. 的不等式
的不等式 的解集为
的解集为 ,求实数
,求实数 的值;
的值; ,若不等式
,若不等式 对任意实数
对任意实数 都成立,求实数
都成立,求实数 的取值范围;
的取值范围; 满足下列条件:
满足下列条件: 时,其最小值为0,且
时,其最小值为0,且 成立;
成立; 时,
时, 恒成立.
恒成立. 的值并求
的值并求 的解析式;
的解析式; ,使得存在
,使得存在 ,只要当
,只要当 时,就有
时,就有 成立.
成立. 的值域为 .
的值域为 . 中,M、N分别是
中,M、N分别是 的中点,则图中阴影部分在平面
的中点,则图中阴影部分在平面 上的投影的面积为 .
上的投影的面积为 .

 在椭圆
在椭圆 上,
上, 、
、 分别是椭圆的两焦点,且
分别是椭圆的两焦点,且 ,则
,则 的面积是( )
的面积是( ) B.
B. C.
C. D.
D.