题目内容
 如图,在四面体ABCD中,已知∠ABD=∠CBD=60°,AB=BC=2,
如图,在四面体ABCD中,已知∠ABD=∠CBD=60°,AB=BC=2,(1)求证:AC⊥BD;
(2)若平面ABD⊥平面CBD,且BD=
| 5 |
| 2 |
考点:二面角的平面角及求法,棱锥的结构特征,空间中直线与直线之间的位置关系
专题:空间位置关系与距离,空间角
分析:(1)由已知得△ABD≌△CBD,从而AD=CD,取AC的中点E,连结BE,DE,则BE⊥AC,DE⊥AC,从而AC⊥平面BED,由此能证明AC⊥BD.
(2)过C作CH⊥BD于点H,由已知得CH⊥平面ABD,过H做HK⊥AD于点K,连接CK,则∠CKH为二面角C-AD-B的平面角,由此能求出二面角C-AD-B的余弦值.
(2)过C作CH⊥BD于点H,由已知得CH⊥平面ABD,过H做HK⊥AD于点K,连接CK,则∠CKH为二面角C-AD-B的平面角,由此能求出二面角C-AD-B的余弦值.
解答:
(1)证明:∵∠ABD=∠CBD,AB=BC,BD=BD.
∴△ABD≌△CBD,
∴AD=CD.
取AC的中点E,连结BE,DE,则BE⊥AC,DE⊥AC.
又∵BE∩DE=E,
BE?平面BED,BD?平面BED,
∴AC⊥平面BED,
∴AC⊥BD.
(2)解:过C作CH⊥BD于点H.则CH?平面BCD,
又∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,
∴CH⊥平面ABD.
过H做HK⊥AD于点K,连接CK.
∵CH⊥平面ABD,∴CH⊥AD,又HK∩CH=H,
∴AD⊥平面CHK,∴CK⊥AD.
∴∠CKH为二面角C-AD-B的平面角.
连接AH.∵△ABD≌△CBD,∴AH⊥BD.
∵∠ABD=∠CBD=60°,AB=BC=2,
∴AH=CH=
,BH=1.∵BD=
,∴DH=
.
∴AD=
,∴HK=
=
.
∴tan∠CKH=
=
,
∴cos∠CKH=
,∴二面角C-AD-B的余弦值为
.

∴△ABD≌△CBD,
∴AD=CD.
取AC的中点E,连结BE,DE,则BE⊥AC,DE⊥AC.
又∵BE∩DE=E,
BE?平面BED,BD?平面BED,
∴AC⊥平面BED,
∴AC⊥BD.
(2)解:过C作CH⊥BD于点H.则CH?平面BCD,
又∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,
∴CH⊥平面ABD.
过H做HK⊥AD于点K,连接CK.
∵CH⊥平面ABD,∴CH⊥AD,又HK∩CH=H,
∴AD⊥平面CHK,∴CK⊥AD.
∴∠CKH为二面角C-AD-B的平面角.
连接AH.∵△ABD≌△CBD,∴AH⊥BD.
∵∠ABD=∠CBD=60°,AB=BC=2,
∴AH=CH=
| 3 |
| 5 |
| 2 |
| 3 |
| 2 |
∴AD=
| ||
| 2 |
| AH•DH |
| AD |
3
| ||
| 7 |
∴tan∠CKH=
| CH |
| HK |
| ||
| 3 |
∴cos∠CKH=
| ||
| 10 |
| ||
| 10 |
点评:本题考查异面直线垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设a,b,c依次是方程x+sinx=1,x+sinx=2,x+
sinx=2的根,并且0<x<
,则a,b,c的大小关系是( )
| 1 |
| 2 |
| π |
| 2 |
| A、a<b<c |
| B、a<c<b |
| C、c<b<a |
| D、b<c<a |
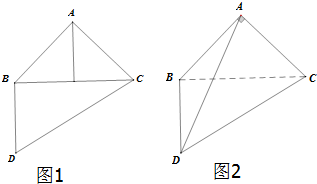 如图1,△ABC是等腰三角形,其中∠A=90°,且DB⊥BC,∠BCD=30°,现将△ABC沿边BC折起,使得二面角A-BC-D大小为30°(如图2),则异面直线BC与AD所成的角为( )
如图1,△ABC是等腰三角形,其中∠A=90°,且DB⊥BC,∠BCD=30°,现将△ABC沿边BC折起,使得二面角A-BC-D大小为30°(如图2),则异面直线BC与AD所成的角为( )| A、30° | B、45° |
| C、60° | D、90° |
已知实数x,y满足
,则z=2x-2y-1的取值范围是( )
|
A、[
| ||
| B、[0,5] | ||
C、[
| ||
D、[-
|