题目内容
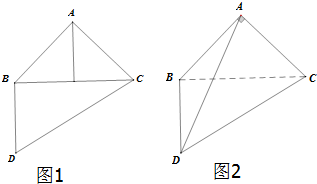 如图1,△ABC是等腰三角形,其中∠A=90°,且DB⊥BC,∠BCD=30°,现将△ABC沿边BC折起,使得二面角A-BC-D大小为30°(如图2),则异面直线BC与AD所成的角为( )
如图1,△ABC是等腰三角形,其中∠A=90°,且DB⊥BC,∠BCD=30°,现将△ABC沿边BC折起,使得二面角A-BC-D大小为30°(如图2),则异面直线BC与AD所成的角为( )| A、30° | B、45° |
| C、60° | D、90° |
考点:二面角的平面角及求法
专题:空间角
分析:设AB=AC=2,则BC=2
,BD=BCtan30°=
,过点C作CM和BD平行且相等,则由题意可得BDMC为矩形,从而∠ADM(或其补角)为异面直线BC与AD所成的角.由此能求出异面直线BC与AD所成的角.
| 2 |
2
| ||
| 3 |
解答:
 解:设AB=AC=2,则BC=2
解:设AB=AC=2,则BC=2
,BD=BCtan30°=
,
过点C作CM和BD平行且相等,则由题意可得BDMC为矩形,
∴∠ADM(或其补角)为异面直线BC与AD所成的角.
取BC中点O,DM中点H,连结AO,HO,
由已知得AO⊥BC,HO⊥BC,
∴∠AOH是二面角A-BC-D的平面角,∴∠AOH=30°,
由已知得AO=
BC=
,HO=BD=
,
∴AH=
=
=
,
又AD=AM,H是DM中点,DH=
BC=
,
∴AH⊥DM,tan∠ADM=
=
=
,
∴∠ADM=30°,
∴异面直线BC与AD所成的角为30°.
故选:A.
 解:设AB=AC=2,则BC=2
解:设AB=AC=2,则BC=2| 2 |
2
| ||
| 3 |
过点C作CM和BD平行且相等,则由题意可得BDMC为矩形,
∴∠ADM(或其补角)为异面直线BC与AD所成的角.
取BC中点O,DM中点H,连结AO,HO,
由已知得AO⊥BC,HO⊥BC,
∴∠AOH是二面角A-BC-D的平面角,∴∠AOH=30°,
由已知得AO=
| 1 |
| 2 |
| 2 |
2
| ||
| 3 |
∴AH=
| AO2+OH2-2AO•OHcos30° |
2+
|
| ||
| 3 |
又AD=AM,H是DM中点,DH=
| 1 |
| 2 |
| 2 |
∴AH⊥DM,tan∠ADM=
| AH |
| DH |
| ||||
|
| ||
| 3 |
∴∠ADM=30°,
∴异面直线BC与AD所成的角为30°.
故选:A.
点评:本题考查异面直线所成角的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
已知回归直线通过样本点的中心,若x与y之间的一组数据:
则y与x的线性回归方程
=
x+
所表示的直线必过点( )
| x | 0 | 1 | 2 | 3 |
| y | 1.1 | 3.1 | 4.9 | 6.9 |
| ∧ |
| y |
| ∧ |
| b |
| ∧ |
| a |
A、(
| ||
| B、(1,2) | ||
| C、(2,2) | ||
D、(
|
设等差数列{an}的前n项和为Sn,若2a8=6+a11,则S9的值等于( )
| A、36 | B、45 | C、54 | D、27 |
设m=|
|,n=|sin
|,则m、n的大小关系为( )
| sinα+sinβ |
| 2 |
| α+β |
| 2 |
| A、m≤n | B、m≥n |
| C、m=n | D、不能确定 |
 如图,P为圆B:(x+2)2+y2=36上一动点,点A坐标为(2,0),线段AP的垂直平分线交直线BP于点Q,求点Q的轨迹方程.
如图,P为圆B:(x+2)2+y2=36上一动点,点A坐标为(2,0),线段AP的垂直平分线交直线BP于点Q,求点Q的轨迹方程.
 如图,在四面体ABCD中,已知∠ABD=∠CBD=60°,AB=BC=2,
如图,在四面体ABCD中,已知∠ABD=∠CBD=60°,AB=BC=2,