题目内容
已知数列{an}:
+
+…+
=n2+n(n∈N*),则数列{an}前n项和Sn= ;.
| a1-1 |
| 2 |
| a2-1 |
| 22 |
| an-1 |
| 2n |
考点:数列的求和
专题:等差数列与等比数列
分析:由已知得
=2n,从而an=1+n•2n+1,进而Sn=1×22+2×23+…+n×2n+1+n,由此利用错位相减法能求出数列{an}前n项和Sn.
| an-1 |
| 2n |
解答:
解:∵
+
+…+
=n2+n(n∈N*),①
∴
+
+…+
=(n-1)2+(n-1),②
①-②得:
=2n,
∴an-1=n•2n+1,
∴an=1+n•2n+1,
∴Sn=1×22+2×23+…+n×2n+1+n,
设Tn=1×22+2×23+…+n×2n+1,③
则2Tn=1×23+2×24+…+n×2n+2,④
③-④,得-Tn=22+23+24+…+2n+1-n×2n+2
=
-n×2n+2,
∴Tn=(n-1)•2n+2+4,
∴Sn=(n-1)•2n+2+n+4.
故答案为:(n-1)•2n+2+n+4.
| a1-1 |
| 2 |
| a2-1 |
| 22 |
| an-1 |
| 2n |
∴
| a1-1 |
| 2 |
| a2-1 |
| 22 |
| an-1-1 |
| 2n-1 |
①-②得:
| an-1 |
| 2n |
∴an-1=n•2n+1,
∴an=1+n•2n+1,
∴Sn=1×22+2×23+…+n×2n+1+n,
设Tn=1×22+2×23+…+n×2n+1,③
则2Tn=1×23+2×24+…+n×2n+2,④
③-④,得-Tn=22+23+24+…+2n+1-n×2n+2
=
| 4(1-2n) |
| 1-2 |
∴Tn=(n-1)•2n+2+4,
∴Sn=(n-1)•2n+2+n+4.
故答案为:(n-1)•2n+2+n+4.
点评:本题考查数列的前n项和的求法,是中档题,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
相关题目
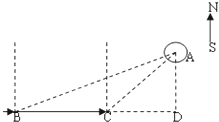 海中一小岛,周围3.8mile内有暗礁,海轮由西向东航行,望见这岛在北偏东80°,航行8n mile以后,望见这岛在北偏东60°,如查这艘海轮不改变航行继续前进,有没有触礁的危险.(精确到0.001,cos10°=0.9848)
海中一小岛,周围3.8mile内有暗礁,海轮由西向东航行,望见这岛在北偏东80°,航行8n mile以后,望见这岛在北偏东60°,如查这艘海轮不改变航行继续前进,有没有触礁的危险.(精确到0.001,cos10°=0.9848)