题目内容
13.已知函数f(x)=Asin(ωx+φ)(A,ω均为正的常数,φ为锐角)的最小正周期为π,当x=$\frac{2π}{3}$时,函数f(x)取得最小值,记a=f(0),b=f($\frac{π}{3}$),c=f($\frac{π}{12}$),则有( )| A. | a=b<c | B. | a<b<c | C. | b<a<c | D. | c<a<b |
分析 根据周期和对称轴作出f(x)的大致图象,根据函数的单调性和对称性判断大小.
解答 解:∵f(x)的周期为π,∴ω=2,
∵A>0,当x=$\frac{2π}{3}$时,函数f(x)取得最小值,∴sin($\frac{4π}{3}$+φ)=-1,∴$\frac{4π}{3}$+φ=-$\frac{π}{2}$+2kπ,
即φ=-$\frac{11π}{6}$+2kπ,∵φ是锐角,∴φ=$\frac{π}{6}$.∴f(x)=Asin(2x+$\frac{π}{6}$).
令A=1,作出f(x)在一个周期内的大致函数图象,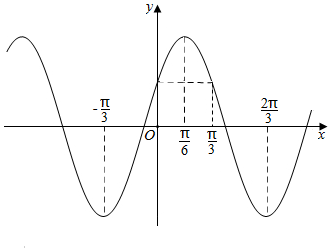
由图象可知f(x)在[0,$\frac{π}{6}$]上单调递增,∴f(0)<f($\frac{π}{12}$),
∵f(x)关于x=$\frac{π}{6}$对称,∴f(0)=f($\frac{π}{3}$),
∴f(0)=f($\frac{π}{3}$)<f($\frac{π}{12}$).
故选:A.
点评 本题考查了正弦函数的图象与性质,属于基础题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
4.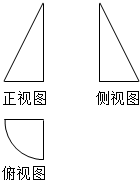 一个几何体的三视图如图所示,其中正视图与侧视图都是斜边长为2的直角三角形,俯视图是半径为1的$\frac{1}{4}$圆周和两条半径,则这个几何体的体积为( )
一个几何体的三视图如图所示,其中正视图与侧视图都是斜边长为2的直角三角形,俯视图是半径为1的$\frac{1}{4}$圆周和两条半径,则这个几何体的体积为( )
 一个几何体的三视图如图所示,其中正视图与侧视图都是斜边长为2的直角三角形,俯视图是半径为1的$\frac{1}{4}$圆周和两条半径,则这个几何体的体积为( )
一个几何体的三视图如图所示,其中正视图与侧视图都是斜边长为2的直角三角形,俯视图是半径为1的$\frac{1}{4}$圆周和两条半径,则这个几何体的体积为( )| A. | $\frac{\sqrt{3}}{12}$π | B. | $\frac{\sqrt{3}}{6}$π | C. | $\frac{\sqrt{3}}{4}$π | D. | $\frac{\sqrt{3}}{3}$π |
8.在△ABC中,a,b,c分别是角A,B,C的对边,且A=$\frac{2π}{3}$,b+2c=8,则当△ABC的面积取得最大值时a的值为( )
| A. | 2$\sqrt{6}$ | B. | 2$\sqrt{7}$ | C. | $\sqrt{14}$ | D. | 4 |
18.若$\left\{\begin{array}{l}{x-y≤0}\\{x+y≤1}\\{x≥0}\end{array}\right.$,则z=x+2y的最小值为( )
| A. | -1 | B. | 0 | C. | $\frac{3}{2}$ | D. | 2 |