题目内容

2．已知函数f（x）=mx2-2x+3，对任意x1，x2∈[-2，+∞）满足$\frac{f（{x}_{1}）-f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＜0，则实数m的取值范围[-$\frac{1}{2}$，0]．

分析 先求出函数的单调性，再通过讨论m的范围，结合二次函数的性质从而求出m的范围即可．

解答 解：对任意x1，x2∈[-2，+∞）满足$\frac{f（{x}_{1}）-f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＜0，
得f（x）在[-2，+∞）单调递减，
当m=0时：f（x）=-2x+3，符合题意，
m≠0时，则m＜0，
此时，对称轴x=-$\frac{-2}{2m}$=$\frac{1}{m}$≤-2，
解得：m≥-$\frac{1}{2}$，
故答案为：[-$\frac{1}{2}$，0]．

点评 本题考察了二次函数的性质，考察函数的单调性问题，考察分类讨论思想，是一道中档题．

练习册系列答案
相关题目
12．已知cos（x-$\frac{π}{4}$）=$\frac{\sqrt{2}}{10}$，x∈（$\frac{π}{2}$，$\frac{3π}{4}$）．
（1）求sinx的值；
（2）求cos（2x-$\frac{π}{3}$）的值．
13．已知函数f（x）=Asin（ωx+φ）（A，ω均为正的常数，φ为锐角）的最小正周期为π，当x=$\frac{2π}{3}$时，函数f（x）取得最小值，记a=f（0），b=f（$\frac{π}{3}$），c=f（$\frac{π}{12}$），则有（　　）
A．a=b＜cB．a＜b＜cC．b＜a＜cD．c＜a＜b
10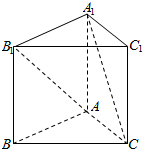．如图，已知正三棱柱ABC-A1B1C1的各条棱长都相等，则异面直线AB1和A1C所成的角的余弦值大小为（　　）
A．$\frac{1}{4}$B．$-\frac{1}{4}$C．$\frac{1}{2}$D．$-\frac{1}{2}$
17．设直线l1：3x+4y-5=0与l2：3x+4y+5=0间的距离为d，则d=2．
7．设0＜α＜π＜β＜2π，向量$\overrightarrow{a}$=（1，2），$\overline{b}$=（2cosα，sinα），$\overrightarrow{c}$=（sinβ，2cosβ），$\overrightarrow{d}$=（cosβ，-2sinβ）．
（1）若$\overrightarrow{a}$⊥$\overrightarrow{b}$，求α；
（2）若|$\overrightarrow{c}$+$\overrightarrow{d}$|=$\sqrt{3}$，求sinβ+cosβ的值；
（3）若tanαtanβ=4，求证：$\overrightarrow{b}$∥$\overrightarrow{c}$．
14．已知m，n是两条不同的直线，α，β是两个不同平面，则以下命题不成立的是（1）（2）（4）
（1）若α∥β，m?α，n?β，则 m∥n
（2）若m∥β，β⊥α，则 m⊥α
（3）若m⊥α，m?β，则 α⊥β
（4）若m∥α，n∥β，m∥n，则 α∥β
11．若f（x）=$\frac{1}{{x}^{2}-2ax+a+5}$在（-2，2）上单调递增，则a的取值范围是[2，3]．
12．设α，β是两个不同的平面，直线m⊥α，则“m⊥β”是“α∥β”的（　　）
A．充分而不必要条件B．必要而不充分条件
C．充分必要条件D．既不充分也不必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网