题目内容
下列命题中,真命题是( )
A、sin(
| ||
| B、常数数列一定是等比数列 | ||
| C、一个命题的逆命题和否命题同真假 | ||
D、x+
|
考点:命题的真假判断与应用
专题:综合题
分析:A、化简sin(
+α)即可;
B、举例说明常数数列不一定是等比数列;
C、一个命题的逆命题和它的否命题是互为逆否命题,真假性相同;
D、x>0时,x+
≥2,x<0时,x+
≤-2.
| 3π |
| 2 |
B、举例说明常数数列不一定是等比数列;
C、一个命题的逆命题和它的否命题是互为逆否命题,真假性相同;
D、x>0时,x+
| 1 |
| x |
| 1 |
| x |
解答:
解:对于A,sin(
+α)=-cosα,∴A错误;
对于B,常数数列不一定是等比数列,如an=0,∴B错误;
对于C,一个命题的逆命题和否命题是互为逆否命题,它们的真假性相同,∴C正确;
对于D,x>0时,x+
≥2,x<0时,x+
=-(-x+
)≤-2,∴D错误.
故选:C.
| 3π |
| 2 |
对于B,常数数列不一定是等比数列,如an=0,∴B错误;
对于C,一个命题的逆命题和否命题是互为逆否命题,它们的真假性相同,∴C正确;
对于D,x>0时,x+
| 1 |
| x |
| 1 |
| x |
| 1 |
| -x |
故选:C.
点评:本题考查了判断命题真假的问题,解题时应对每一个命题进行分析,以便得出正确的答案.

练习册系列答案
相关题目
函数f(x)=4x2-mx+5在区间[-2,+∞)上是增函数,则( )
| A、f (1)≥25 |
| B、f (1)=25 |
| C、f (1)≤25 |
| D、f (1)>25 |
关于函数y=
的单调性的叙述正确的是( )
| -3 |
| x |
| A、在(-∞,0)上是增函数,在(0,+∞) 上是减函数 |
| B、在(-∞,0)∪(0,+∞)上是增函数 |
| C、在[0,+∞)上是增函数 |
| D、在上(-∞,0)和(0,+∞)是增函数 |
已知F1(-3,0),F2(3,0),动点P满足:|PF1|+|PF2|=6,则动点P的轨迹为( )
| A、椭圆 | B、抛物线 |
| C、线段 | D、双曲线 |
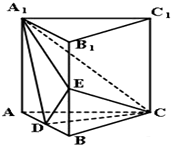 如图:直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°.E为的中点,D点在AB上且DE=
如图:直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°.E为的中点,D点在AB上且DE=