题目内容
已知函数f(x)=x2-ax-alnx(a∈R).
(1)若函数f(x)在x=1处取得极值,求a的值.
(2)在(1)的条件下,求证:f(x)≥-
+
-4x+
;
(3)当x∈[e,+∞),f(x)≥0恒成立,求a的取值范围.
(1)若函数f(x)在x=1处取得极值,求a的值.
(2)在(1)的条件下,求证:f(x)≥-
| x3 |
| 3 |
| 5x2 |
| 2 |
| 11 |
| 6 |
(3)当x∈[e,+∞),f(x)≥0恒成立,求a的取值范围.
考点:利用导数研究曲线上某点切线方程,函数恒成立问题
专题:综合题,导数的综合应用
分析:(1)求导数,利用函数f(x)在x=1处取得极值,可得f′(1)=0,即可求a的值.
(2)构造g(x)=f(x)-(-
+
-4x+
),可知g(x)在(0,1)上是减函数,在(1,+∞)上是增函数,即可证明结论;
(3)当x∈[e,+∞),f(x)≥0恒成立,等价于a≤
在x∈[e,+∞)时恒成立,求最值,即可求a的取值范围.
(2)构造g(x)=f(x)-(-
| x3 |
| 3 |
| 5x2 |
| 2 |
| 11 |
| 6 |
(3)当x∈[e,+∞),f(x)≥0恒成立,等价于a≤
| x2 |
| x+lnx |
解答:
(1)解:f′(x)=2x-a-
,由题意可得f′(1)=0,解得a=1;
经检验,a=1时f(x)在x=1处取得极值,所以a=1.(3分)
(2)证明:由(1)知,f(x)=x2-x-lnx.
令g(x)=f(x)-(-
+
-4x+
)=
-
+3x-lnx-
,
由g′(x)=x2-3x+3-
=
-3(x-1)=
(x>0),
可知g(x)在(0,1)上是减函数,在(1,+∞)上是增函数,
所以g(x)≥g(1)=0,所以f(x)≥-
+
-4x+
成立;(8分)
(3)解:由x∈[e,+∞)知,x+lnx>0,
所以f(x)≥0恒成立等价于a≤
在x∈[e,+∞)时恒成立,
令h(x)=
,x∈[e,+∞),有h′(x)=
>0,
所以h(x)在[e,+∞)上是增函数,有h(x)≥h(e)=
,所以a≤
.(12分)
| a |
| x |
经检验,a=1时f(x)在x=1处取得极值,所以a=1.(3分)
(2)证明:由(1)知,f(x)=x2-x-lnx.
令g(x)=f(x)-(-
| x3 |
| 3 |
| 5x2 |
| 2 |
| 11 |
| 6 |
| x3 |
| 3 |
| 3x2 |
| 2 |
| 11 |
| 6 |
由g′(x)=x2-3x+3-
| 1 |
| x |
| x3-1 |
| x |
| (x-1)3 |
| x |
可知g(x)在(0,1)上是减函数,在(1,+∞)上是增函数,
所以g(x)≥g(1)=0,所以f(x)≥-
| x3 |
| 3 |
| 5x2 |
| 2 |
| 11 |
| 6 |
(3)解:由x∈[e,+∞)知,x+lnx>0,
所以f(x)≥0恒成立等价于a≤
| x2 |
| x+lnx |
令h(x)=
| x2 |
| x+lnx |
| x(x-1+2lnx) |
| (x+lnx)2 |
所以h(x)在[e,+∞)上是增函数,有h(x)≥h(e)=
| e2 |
| e+1 |
| e2 |
| e+1 |
点评:本小题主要考查函数与导数的综合应用能力,具体涉及到用导数来描述原函数的单调性、极值的情况.本小题对考生的逻辑推理能力与运算求解有较高要求.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
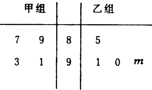 如图所示茎叶图记录了甲、乙两学习小组各4名同学在某次考试中的数学成绩,乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中用m(m∈N)表示.
如图所示茎叶图记录了甲、乙两学习小组各4名同学在某次考试中的数学成绩,乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中用m(m∈N)表示. 如图,平行四边形ABCD中,E、F分别是AD,AB的中点,G为BE与DF的交点.若
如图,平行四边形ABCD中,E、F分别是AD,AB的中点,G为BE与DF的交点.若 如图,椭圆E:
如图,椭圆E: