题目内容
已知数列{an}是等差数列,a2=6,a5=12,数列{bn}的前n项和是Sn,且Sn+
bn=1.
(1)求数列{an}的通项公式;
(2)求证:数列{bn}是等比数列;
(3)记cn=
,{cn}的前n项和为Tn,若Tn<
对一切n∈N+都成立,求最小正整数m.
| 1 |
| 2 |
(1)求数列{an}的通项公式;
(2)求证:数列{bn}是等比数列;
(3)记cn=
| -2 | ||
anlog3
|
| m-2013 |
| 2 |
考点:数列的求和,等比关系的确定
专题:等差数列与等比数列
分析:(1)由已知条件利用等差数列通项公式列出方程组,求出首项和公差,由此能求出{an}的通项公式.
(2)由已知得当n=1时,b1+
b1=1,当n≥2时,Sn+
bn=1,Sn-1+
bn-1=1,从而能够证明{bn}是以
为首项,公比为
的等比数列.
(3)由bn=2•(
)n,得cn=
=
=
-
,由此利用裂项求和法能求出最小正整数m.
(2)由已知得当n=1时,b1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
(3)由bn=2•(
| 1 |
| 3 |
| -2 | ||
anlog3
|
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
解答:
(1)解:设{an}的公差为d,
则a2=a1+d=6,a5=a1+4d=12,
解得:a1=4,d=2,
∴an=4+(n-1)×2=2n+2.…(2分)
(2)证明:∵数列{bn}的前n项和是Sn,且Sn+
bn=1,
∴当n=1时,b1+
b1=1,解得b1=
,…(4分)
当n≥2时,Sn+
bn=1,Sn-1+
bn-1=1,
两式相减,得bn+
bn-
bn-1=0,…(5分)
∴bn=
bn-1,…(6分)
∴{bn}是以
为首项,公比为
的等比数列…(7分)
(3)解:由(2)可知:bn=
•(
)n-1=2•(
)n,…(8分)
∴cn=
=
=
=
-
,
∴Tn=1-
+
-
+
-
+…+(
-
)=1-
<1.…(12分)
∵Tn<
对一切n∈N+都成立,
∴
≥1,解得m≥2015,∴最小正整数m=2015.…(14分)
则a2=a1+d=6,a5=a1+4d=12,
解得:a1=4,d=2,
∴an=4+(n-1)×2=2n+2.…(2分)
(2)证明:∵数列{bn}的前n项和是Sn,且Sn+
| 1 |
| 2 |
∴当n=1时,b1+
| 1 |
| 2 |
| 2 |
| 3 |
当n≥2时,Sn+
| 1 |
| 2 |
| 1 |
| 2 |
两式相减,得bn+
| 1 |
| 2 |
| 1 |
| 2 |
∴bn=
| 1 |
| 3 |
∴{bn}是以
| 2 |
| 3 |
| 1 |
| 3 |
(3)解:由(2)可知:bn=
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴cn=
| -2 | ||
anlog3
|
| -2 | ||
(2n+2)log3(
|
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Tn=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
∵Tn<
| m-2013 |
| 2 |
∴
| m-2013 |
| 2 |
点评:本题考查数列的通项公式的求法,考查等比数列的证明,考查满足条件的最小正整数的求法,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
相关题目
设数列{an}的前n项和为Sn,且a1=a2=1,{nSn+(n+2)an}为等差数列,则an=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
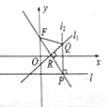 如图,在平面直角坐标系xOy中,点F(0,1),直线l:y=-1,点P在直线l上移动,R是线段PF与x轴的交点,过点R,P分别作直线l1,l2,使得l1⊥PF,l2⊥l,l1∩l2=Q.
如图,在平面直角坐标系xOy中,点F(0,1),直线l:y=-1,点P在直线l上移动,R是线段PF与x轴的交点,过点R,P分别作直线l1,l2,使得l1⊥PF,l2⊥l,l1∩l2=Q.