题目内容
19.等差数列{an}的首项a1=1,公差d≠0,且a3•a4=a12.(1)求数列{an}的通项公式;
(2)设bn=an•2n,求数列{bn}的前n项和Tn.
分析 (1)由已知a3•a4=a12,求得d=1,即可写出通项公式;
(2)bn=an•2n=n•2n,数列{bn}的前n项和Tn,Tn=b1+b2+b3+…+bn,采用乘以公比错位相减法,求得Tn.
解答 解:a3•a4=a12.
(a1+2d)(a1+3d)=(a1+11d),
解得:d=1,
an=n,
数列{an}的通项公式,an=n;
bn=an•2n=n•2n,
数列{bn}的前n项和Tn,Tn=1×2+2×22+3×23+…+n•2n,
2Tn=1×22+2×23+3×24+…+(n-1)•2n+n•2n+1,
两式相减得:-Tn=2+22+23+…+2n-n•2n+1,
Tn=n•2n+1-2n+1+2=(n-1)2n+1+2
∴Tn=(n-1)2n+1+2.
点评 本题考查求数列的通项公式和乘以公比错位相减法,是高考的重点,要求学生熟练运用错位相减法,属于中档题.

练习册系列答案
相关题目
7.“|x-1|<2成立”是“x(x-3)<0成立”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不不充分也不必要条件 |
8.某单位老年人、中年人、青年人的人数如表,用分层抽样的方法抽取17人进行单位管理问卷调查,其中抽到3位老年人,则抽到的中年人人数为( )
| 类别 | 人数 |
| 老年人 | 15 |
| 中年人 | ? |
| 青年人 | 40 |
| A. | 9 | B. | 8 | C. | 6 | D. | 3 |
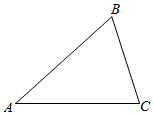 如图,在△ABC中,∠B=$\frac{π}{3}$,AC=2$\sqrt{3}$.
如图,在△ABC中,∠B=$\frac{π}{3}$,AC=2$\sqrt{3}$.