题目内容
双曲线的实轴长与虚轴长之和等于其焦距的
倍,且一个顶点的坐标为(0,2),则双曲线的标准方程为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:由已知得双曲线的标准方程为
-
=1,且2a+2b=
•2c,由此能求出双曲线方程.
| y2 |
| 4 |
| x2 |
| b2 |
| 2 |
解答:
解:∵双曲线的顶点坐标为(0,2),
∴a=2,且双曲线的标准方程为
-
=1.
根据题意2a+2b=
•2c,即a+b=
c.
又a2+b2=c2,且a=2,
∴解上述两个方程,得b2=4.
∴符合题意的双曲线方程为
-
=1.
故选:B.
∴a=2,且双曲线的标准方程为
| y2 |
| 4 |
| x2 |
| b2 |
根据题意2a+2b=
| 2 |
| 2 |
又a2+b2=c2,且a=2,
∴解上述两个方程,得b2=4.
∴符合题意的双曲线方程为
| y2 |
| 4 |
| x2 |
| 4 |
故选:B.
点评:本题考查双曲线方程的求法,是基础题,解题时要认真审题,注意双曲线性质的合理运用.

练习册系列答案
相关题目
若角α的终边在直线y=2x上,则sinα等于( )
A、±
| ||||
B、±
| ||||
C、±
| ||||
D、±
|
观察如图:

若第n行的各数之和等于20112,则n=( )

若第n行的各数之和等于20112,则n=( )
| A、2011 | B、2012 |
| C、1006 | D、1005 |
已知数列{an}的通项为an=
,则数列{an}的最大项为( )
| n |
| n2+58 |
| A、第7项 | B、第8项 |
| C、第7项或第8项 | D、不存在 |
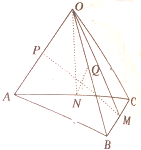 如图,已知空间四边形OABC中,M为BC中点,N为AC中点,P为OA中点,Q为OB中点,若AB=OC,求证:PM⊥QN.
如图,已知空间四边形OABC中,M为BC中点,N为AC中点,P为OA中点,Q为OB中点,若AB=OC,求证:PM⊥QN.