题目内容

已知向量
a
，
b
，
c
满足|
a
|=|
b
|=2，|
c
|=1，（
c
-
a
）（
c
-
b
）=0，则
a
•
b
的取值范围是
 
．
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：由条件化简向量等式，注意运用向量的平方即为模的平方和向量的数量积的定义和性质，转化为不等式，解得即可得到范围．
解答： 解：由于|
a
|=|
b
|=2，|
c
|=1，
则（
c
-
a
）（
c
-
b
）=0，
即为
c
2-（
a
+
b
）•
c
+
a
•
b
=0，
即有
a
•
b
=（
a
+
b
）•
c
-1=|
a
+
b
|•|
c
|•cos＜
a
+
b
，
c
＞-1≤|
a
+
b
|-1=
a
2+
b
2+2
a
•
b
-1=
8+2
a
•
b
-1，
即有（1+
a
•
b
）2≤8+2
a
•
b
，
即为（
a
•
b
）2≤7，
解得，-
7
≤
a
•
b
≤
7
．
故答案为：[-
7
，
7
]．
点评：本题考查平面向量的数量积的定义和性质，考查向量的平方即为模的平方，考查运算能力，属于中档题．
练习册系列答案
相关题目
已知α是第四象限角，且sinα=-
4
5
，则tan2α的值为（　　）
A、-
4
3
B、-
24
7
C、
24
7
D、
24
25
已知f(x)=sin(-2x+
π
6
)求：
（1）函数的最小正周期；
（2）函数的单调增区间；
（3）若-
π
3
≤x≤
π
6
，求函数的值域．
过点（0，4）作直线，使它与抛物线y2=4x仅有一个公共点，这样的直线有（　　）
A、1条B、2条C、3条D、4条
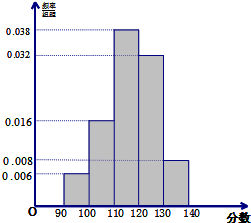某校50名学生参加2013年全国数学联赛初赛，成绩全部介于90分到140分之间．将成绩结果按如下方式分成五组：第一组[90，100），第二组[100，110），第五组[130，140]．按上述分组方法得到的频率分布直方图如图所示．
（1）若成绩大于或等于100分且小于120分认为是良好的，求该校参赛学生在这次数学联赛中成绩良好的人数；
（2）若从第一、五组中共随机取出两个成绩，求这两个成绩差的绝对值大于30分的概率．
已知函数f（x）=x3+x2+|x-a|．（a是常数，且a≤
1
3
）
（Ⅰ）讨论f（x）的单调性；
（Ⅱ）当-2≤x≤1时，f（x）的最小值为g（a），求证：对任意x∈[-2，1]，f（x）≤g（a）+9成立．
若函数f（x）=|x-3|-logax+1无零点，则a的取值范围为
 
．
已知x，y∈R，则“x•y＞0”是“x＞0且y＞0”的（　　）
A、充分不必要条件
B、必要不充分条件
C、充要条件
D、既不充分也不必要条件
双曲线的实轴长与虚轴长之和等于其焦距的
2
倍，且一个顶点的坐标为（0，2），则双曲线的标准方程为（　　）
A、
x2
4
-
y2
4
=1
B、
y2
4
-
x2
4
=1
C、
y2
4
-
x2
8
=1
D、
x2
8
-
y2
4
=1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网