题目内容
已知直线y=x-4与f(x)=loga(-x)和g(x)=a-x(a>1)的图象分别交于A(x1,y1),B(x2,y2),则x1+x2= .
考点:函数的图象
专题:函数的性质及应用
分析:先做出函数f(x)=loga(-x)和g(x)=a-x(a>1)的图象,由互为反函数的两函数图象性质可知,它们关于直线y=-x对称,而直线y=x-4垂直于直线y=-x,则直线y=x-4与两曲线的交点A,B关于直线y=-x对称,也就是关于两直线的交点对称,只需求出两直线的交点,结合中点坐标公式即可求出结果.
解答:
解:∵函数y=ax(a>1)与函数y=logax(a>1)互为反函数,
∴它们的图象关于直线y=x对称,
将分别作出函数y=ax(a>1)与函数y=logax(a>1)图象关于y轴对称的图象,
则得到f(x)=loga(-x)和g(x)=a-x(a>1)的图象,且它们的图象关于直线y=-x对称,
而直线y=x-4垂直于直线y=-x,
∴f(x)=loga(-x)和g(x)=a-x(a>1)的图象与直线y=x-4的交点A、B也关于直线y=-x对称,
即A、B两点关于直线y=x-4与y=-x的交点P对称,∴P是A、B的中点,
又由
得交点为P(2,-2),
∴x1+x2=4.
故答案为4
∴它们的图象关于直线y=x对称,
将分别作出函数y=ax(a>1)与函数y=logax(a>1)图象关于y轴对称的图象,
则得到f(x)=loga(-x)和g(x)=a-x(a>1)的图象,且它们的图象关于直线y=-x对称,
而直线y=x-4垂直于直线y=-x,
∴f(x)=loga(-x)和g(x)=a-x(a>1)的图象与直线y=x-4的交点A、B也关于直线y=-x对称,
即A、B两点关于直线y=x-4与y=-x的交点P对称,∴P是A、B的中点,
又由
|
∴x1+x2=4.
故答案为4
点评:这道题考查了同底数的指数、对数函数互为反函数的图象性质,图象的对称变换等知识,以及利用数形结合的思想解题的能力.

练习册系列答案
相关题目
已知x,y都是正数,且xy=1,则x+y的最小值为( )
| A、4 | B、3 | C、2 | D、1 |
下列命题正确的是( )
| A、ac<bc⇒a<b | ||||
B、若a<b<0,则,
| ||||
C、当x>0且x≠1时,lgx+
| ||||
D、
|
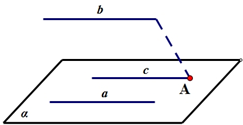 已知直线a在平面α上,直线b不在平面α上,且a∥b,求证:b∥α.
已知直线a在平面α上,直线b不在平面α上,且a∥b,求证:b∥α.