题目内容
若两个函数的图象仅经过若干次平移能够重合,则称这两个函数为“同形”函数,给出下列三个函数:f1(x)=2cos2x,f2(x)=sinx+
cosx,f3(x)=2cos(x-
)-1,则( )
| 3 |
| π |
| 3 |
| A、f1(x),f2(x),f3(x)两两为“同形”函数 |
| B、f1(x),f2(x),f3(x)两两不为“同形”函数 |
| C、f1(x),f2(x)为“同形”函数,且它们与f3(x) 不为“同形”函数 |
| D、f2(x),f3(x)为“同形”函数,且它们与f1(x) 不为“同形”函数 |
考点:两角和与差的正弦函数
专题:三角函数的图像与性质
分析:利用两角和公式对函数f2(x)进行化简,通过对比周期可知f1(x) 与f2(x)和f3(x)不为“同形”函数.通过函数图象的平移法则可知f2(x)图象平移后可与f3(x)的图象重合,推断出f2(x),f3(x)为“同形”函数.
解答:
解:f2(x)=sinx+
cosx=2sin(x+
)=2cos(x-
),
f3(x)=2cos(x-
)-1,
f1(x)的周期为π,f2(x)和f3(x)的周期为2π,
∴f1(x)的图象与f2(x)和f3(x)的图象平移后不可能重合.f1(x) 与二者不为“同形”函数.
f2(x)图象向右平移
个单位,再向下平移一个单位即可与f3(x)的图象重合,
∴f2(x),f3(x)为“同形”函数,
故选:D.
| 3 |
| π |
| 3 |
| π |
| 6 |
f3(x)=2cos(x-
| π |
| 3 |
f1(x)的周期为π,f2(x)和f3(x)的周期为2π,
∴f1(x)的图象与f2(x)和f3(x)的图象平移后不可能重合.f1(x) 与二者不为“同形”函数.
f2(x)图象向右平移
| π |
| 6 |
∴f2(x),f3(x)为“同形”函数,
故选:D.
点评:本题主要考查了两角和与差的正弦函数的公式,三角函数图象的平移变换.考查了学生推理能力.

练习册系列答案
相关题目
在复数范围内,方程x2=-1的解是( )
| A、±1 | B、-1 | C、±i | D、i |
△ABC所在平面α外一点P到三角形三顶点的距离相等,那么点P在α内的射影一定是△ABC的( )
| A、外心 | B、内心 |
| C、重心 | D、以上都不对 |
将两个数a=2,b=-1交换,使a=-1,b=2,下列语句正确的是( )
A、 |
B、 |
C、 |
D、 |
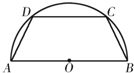 如图,半径为2的半圆有一内接梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.若双曲线以A,B为焦点,且过C,D两点,则当梯形ABCD的周长最大时,双曲线的实轴长为( )
如图,半径为2的半圆有一内接梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.若双曲线以A,B为焦点,且过C,D两点,则当梯形ABCD的周长最大时,双曲线的实轴长为( )A、
| ||
B、2
| ||
C、
| ||
D、2
|
 定义某种运算?,S=a?b的运算原理如图所示.设f(x)=(0?x)x-(3?x).则f(3)=
定义某种运算?,S=a?b的运算原理如图所示.设f(x)=(0?x)x-(3?x).则f(3)=